第109页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
8. [2025 保定校级模拟]如图,△ABC 与△DEF 关于点 O 成中心对称,连接 AD,BE,CF. 下列结论中正确的有(
①点 A 与点 D 是对应点;
②△ACO ≌ △DFO;
③线段 AB 与 DE 关于点 O 成中心对称.
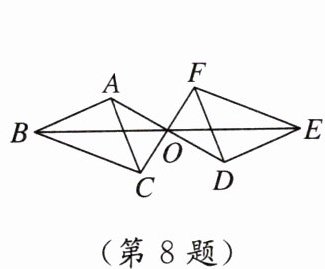
A.0 个
B.1 个
C.2 个
D.3 个
D
)①点 A 与点 D 是对应点;
②△ACO ≌ △DFO;
③线段 AB 与 DE 关于点 O 成中心对称.

A.0 个
B.1 个
C.2 个
D.3 个
答案:
D
9. 如图,已知四边形 ABCD 与四边形 EFGH 关于直线 BD 上的某个点成中心对称,则点 B 的对称点是(

A.点 E
B.点 F
C.点 G
D.点 H
D
)
A.点 E
B.点 F
C.点 G
D.点 H
答案:
D
10. 如图,已知△ABM 与△ACM 关于直线 AF 成轴对称,△ABE 与△DCE 关于点 E 成中心对称,点 E,D,M 都在线段 AF 上,BM 的延长线交 CF 于点 P.
(1)求证:AC = CD;
(2)若∠BAC = 2∠MPC,请你判断∠F 与∠MCD 的数量关系,并说明理由.
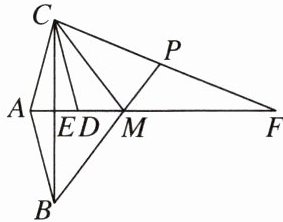
(1)求证:AC = CD;
(2)若∠BAC = 2∠MPC,请你判断∠F 与∠MCD 的数量关系,并说明理由.

答案:
(1)[证明]
∵△ABM与△ACM关于直线AF成轴对称,
∴△ABM≌△ACM.
∴AB=AC.
∵△ABE与△DCE关于点E成中心对称,
∴△ABE≌△DCE.
∴AB=CD.
∴AC=CD.(2)[解]∠F=∠MCD.理由如下: 由(1)可得△ABM≌△ACM,△ABE≌△DCE.
∴∠BAE=∠CAE=∠CDE,∠CMA=∠BMA.
∵∠BAC=2∠MPC,∠BMA=∠PMF,
∴设∠MPC=α,则∠BAC=2α,即∠BAE=∠CAE=∠CDE = α. 设∠BMA=β,则∠PMF=∠CMA=β.
∴∠F=∠MPC - ∠PMF = α - β, ∠MCD=∠CDE - ∠DMC = α - β.
∴∠F=∠MCD.
∵△ABM与△ACM关于直线AF成轴对称,
∴△ABM≌△ACM.
∴AB=AC.
∵△ABE与△DCE关于点E成中心对称,
∴△ABE≌△DCE.
∴AB=CD.
∴AC=CD.(2)[解]∠F=∠MCD.理由如下: 由(1)可得△ABM≌△ACM,△ABE≌△DCE.
∴∠BAE=∠CAE=∠CDE,∠CMA=∠BMA.
∵∠BAC=2∠MPC,∠BMA=∠PMF,
∴设∠MPC=α,则∠BAC=2α,即∠BAE=∠CAE=∠CDE = α. 设∠BMA=β,则∠PMF=∠CMA=β.
∴∠F=∠MPC - ∠PMF = α - β, ∠MCD=∠CDE - ∠DMC = α - β.
∴∠F=∠MCD.
11. 下图是“弦图”,请将“弦图”中的四个直角三角形通过你所学过的图形变换,在以下方格纸中设计另两个不同的图案.


答案:
[解]如图所示.(答案不唯一)

[解]如图所示.(答案不唯一)


12. 图①是利用正方形各边中点和弧的中点设计的正方形瓷砖图案,用四块如图①所示的正方形瓷砖拼成一个新的正方形,使拼成的图案既是轴对称图形,又是中心对称图形. 请你在图②和图③中各画一种拼法.


答案:
[解]如图①②所示,答案不唯一.
[解]如图①②所示,答案不唯一.

13. 如图,把一张长方形纸片 ABCD 沿 EF 折叠后,点 D,C 分别落在点 D',C'的位置上,D'E 与 BC 相交于点 G,若∠CFC' = 110°,求∠AEG 和∠FGD'的度数.


答案:
[解]由折叠知∠C'FE=∠CFE,∠D'EF=∠DEF.
∵∠CFC' = 110°,
∴∠CFE=(360° - 110°)÷2 = 125°.
∴∠GFE=55°.由题易知BC//AD,
∴∠DEF=∠GFE = 55°.
∴∠D'EF=55°.
∴∠AEG=180° - ∠D'EF - ∠DEF = 180° - 55° - 55° = 70°,∠FGD'=∠GEF + ∠GFE = 55° + 55° = 110°.
∵∠CFC' = 110°,
∴∠CFE=(360° - 110°)÷2 = 125°.
∴∠GFE=55°.由题易知BC//AD,
∴∠DEF=∠GFE = 55°.
∴∠D'EF=55°.
∴∠AEG=180° - ∠D'EF - ∠DEF = 180° - 55° - 55° = 70°,∠FGD'=∠GEF + ∠GFE = 55° + 55° = 110°.
查看更多完整答案,请扫码查看


