《2025年综合应用创新题典中点八年级数学上册冀教版》

1. [2024 德州] 在 $0,\frac{1}{2},-2,\sqrt{2}$ 这四个数中,最小的数是(C)
A.$0$
B.$\frac{1},{2}$
C.$-2$
D.$\sqrt{2}$

答案： C

2. [2025 衡水月考] 三个数 $-\pi,-3,-\sqrt{3}$ 的大小关系是(B)
A.$-\sqrt{3}＜-\pi＜-3$
B.$-\pi＜-3＜-\sqrt{3}$
C.$-3＜-\pi＜-\sqrt{3}$
D.$-3＜-\sqrt{3}＜-\pi$

答案： B

3. 估计 $\sqrt{8}$ 的值在(B)
A.$1$ 和 $2$ 之间
B.$2$ 和 $3$ 之间
C.$3$ 和 $4$ 之间
D.$4$ 和 $5$ 之间

答案： B

4. 下列整数中,与 $2-\sqrt{2}$ 最接近的是(C)
A.$-1$
B.$0$
C.$1$
D.$2$

答案： C

5. 实数 $a,b$ 在数轴上对应点的位置如图所示,下列结论正确的是(D)

A.$|a|＞|b|$
B.$a + b＜0$
C.$a + 2＞b + 2$
D.$|a - 1|＞|b - 1|$

答案： D

6. [2024·滨州] 写出一个比 $\sqrt{3}$ 大且比 $\sqrt{10}$ 小的整数2(答案不唯一)。

答案： 2(答案不唯一)

7. 比较下列各组数的大小：
$-\sqrt{4}$＞$-\sqrt{5}$；$\sqrt{7}$______＞$4-\sqrt{3}$；
$\sqrt{11}$＞$3\frac{1},{5}$；$-\sqrt{5}$______＜$-2.23$。

答案： ＞;＞;＞;＜

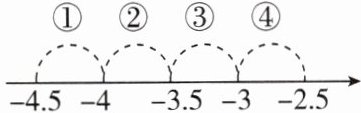
8. 如图,在数轴上标注了四段范围,则表示 $-\sqrt{10}$ 的点落在第③段(填序号).

答案： ③ 【点拨】
∵9＜10＜16,
∴3＜√10＜4.
∵3.5²=12.25＞10,
∴3＜√10＜3.5.
∴-3.5＜-√10＜-3.
∴由图可知表示-√10的点落在第③段.

9. 在解答题目“在如图所示的数轴上标出 $-\pi,\sqrt{9},\sqrt{5},-1$,再比较这四个数的大小”时,嘉淇已经标出了 $-\pi$ 和 $\sqrt{5}$,请你标出其余两个数,并比较这四个数的大小.

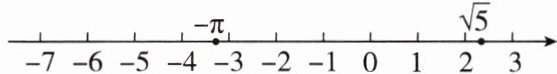
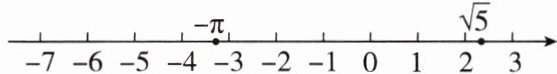
答案：
【解】
∵√4＜√5＜√9,
∴2＜√5＜3,结合-4＜-π＜-3,√9=3,可知√9,-1标在数轴上如图所示:由-π,√9,√5,-1在数轴上的位置可知-π＜-1＜√5＜√9.

10. [2025 保定月考] 若 $6＜a\sqrt{3}＜7$,则 $a$ 的值可能是(C)
A.$2$
B.$3$
C.$4$
D.$5$

答案： C

11. 设 $A,B$ 均为实数,且 $A= \sqrt{5 - m},B= \sqrt[3]{m - 5}$,则 $A,B$ 的大小关系是(D)
A.$A＞B$
B.$A = B$
C.$A＜B$
D.$A\geqslant B$

答案： D 【点拨】
∵A=√5-m,
∴A是一个非负数,且5-m≥0.
∴m≤5.
∴m-5≤0.又
∵B=³√m-5,
∴B≤0.
∴A≥B,故选D.

12. 若将四个数 $-\sqrt{3},\sqrt{7},\sqrt{10},\pi - 1$ 表示在数轴上,其中能被如图所示的墨迹覆盖的数是√7,π-1。

答案： √7,π-1

13. [2024 河北] 已知 $a,b,n$ 均为正整数.
(1)若 $n＜\sqrt{10}＜n + 1$,则 $n=$3；
(2)若 $n - 1＜\sqrt{a}＜n,n＜\sqrt{b}＜n + 1$,则满足条件的 $a$ 的个数总比 $b$ 的个数少2个.

答案：
(1)3 【点拨】
∵√9＜√10＜√16,
∴3＜√10＜4.
∵n＜√10＜n+1,n为正整数,
∴n=3.
(2)2 【点拨】
∵n-1＜√a＜n,
∴(n-1)²＜a＜n².
∴a的个数为n²-(n-1)²-1=n²-n²+2n-1-1=2n-2.
∵n＜√b＜n+1,
∴n²＜b＜(n+1)².
∴b的个数为(n+1)²-n²-1=n²+2n+1-n²-1=2n.
∵2n-(2n-2)=2,
∴满足条件的a的个数总比b的个数少2个.

14. 规定：$[x]$ 表示不超过 $x$ 的最大整数. 如：$[3.2]= 3,[\sqrt{8}]= 2$. 那么 $[\sqrt{1}]+[\sqrt{2}]+[\sqrt{3}]+[\sqrt{4}]+…+[\sqrt{61}]+[\sqrt{62}]$ 的值为301。

答案： 301 【点拨】
∵√1=1,√4=2,√9=3,√16=4,√25=5,√36=6,√49=7,√64=8,
∴[√1]=[√2]=[√3]=1,[√4]=[√5]=[√6]=[√7]=[√8]=2,…,[√49]=[√50]=…=[√61]=[√62]=7.
∴[√1]+[√2]+[√3]+[√4]+…+[√61]+[√62]=1×3+2×5+3×7+4×9+5×11+6×13+7×14=3+10+21+36+55+78+98=301.