《2025年综合应用创新题典中点八年级数学上册冀教版》

1. 下列说法错误的是(B)

A.±3 是 9 的平方根
B.$\sqrt{16}$ 的平方根为 ±4
C.25 的平方根为 ±5
D.负数没有平方根

答案： B

2. 若一个正数 $m$ 的两个不同的平方根分别是 $2a - 5$ 和 $4 - a$,则 $m$ 的值为(C)
A.1
B.3
C.9
D.81

答案： C

3. 新考法 分类讨论法 已知 9,16 和 $a$ 三个数,使这三个数中的一个数是另外两个数乘积的一个平方根,写出所有符合条件的数 $a$ 的值：±12，$\frac{81}{16}$，$\frac{256}{9}$.

答案： ±12，$\frac{81}{16}$，$\frac{256}{9}$ [点拨]分情况讨论:①$a^{2}=9×16$，解得$a=±12$；②$16a=9^{2}$，解得$a=\frac{81}{16}$；③$9a=16^{2}$，解得$a=\frac{256}{9}$。综上，a的值为±12，$\frac{81}{16}$，$\frac{256}{9}$。

4. 求下列各式中 $x$ 的值：
(1) $25x^2 - 16 = 0$；
(2) $(2x + 1)^2 = 169$.

答案： [解]
(1)$x=±\frac{4}{5}$。
(2)$x=6$或$x=-7$。

5. 实数 225 的算术平方根为(A)
A.15
B.$\sqrt{15}$
C.±$\sqrt{15}$
D.±15

答案： A

6. 化简 $\sqrt{(-\frac{1}{7})^2}$ 的值为(A)
A.$\frac{1}{7}$
B.-$\frac{1}{7}$
C.±$\frac{1}{7}$
D.$\frac{1}{49}$

答案： A

7. 已知 $y = \sqrt{a - 2} + \sqrt{3(b + 1)}$,当 $y$ 最小时,$b^a$ 的算术平方根为1.

答案： 1

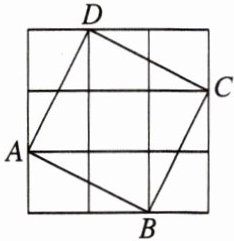
8. 如图,在 $3×3$ 的方格中(每个小正方形的边长为 1),四边形 $ABCD$ 是正方形,利用面积的关系探求正方形 $ABCD$ 的边长是______.
]

答案：
$\sqrt{5}$ [点拨]如图,
∵$S_{正方形ABCD}=S_{正方形EFGH}-S_{\triangle ADE}-S_{\triangle AFB}-S_{\triangle BGC}-S_{\triangle CHD}=3×3-\frac{1}{2}×2×1-\frac{1}{2}×2×1-\frac{1}{2}×2×1-\frac{1}{2}×2×1=9-1-1-1-1=5$，
∴正方形ABCD的边长是$\sqrt{5}$。

9. 新趋势、最值探究题 已知实数 $a$,$b$ 满足 $3\sqrt{a - 1} + 5|b| = 9$,$s = \sqrt{a - 1} + \frac{3}{2}|b|$,则 $w = 18s + 1$ 的最大值为55.

答案： 55 [点拨]
∵$3\sqrt{a - 1}+5|b|=9$，
∴$\sqrt{a - 1}=\frac{9 - 5|b|}{3}$。
∵$\sqrt{a - 1}≥0$，
∴$|b|≤\frac{9}{5}$。
∵$s=\sqrt{a - 1}+\frac{3}{2}|b|$，
∴$s=\frac{9 - 5|b|}{3}+\frac{3}{2}|b|=3-\frac{1}{6}|b|$。又
∵$0≤|b|≤\frac{9}{5}$，
∴$\frac{27}{10}≤s≤3$。又
∵$w = 18s + 1$，
∴$\frac{27}{10}×18 + 1≤w≤18×3 + 1$。
∴$49.6≤w≤55$。
∴w的最大值为55。

10. -125 的立方根为(A)

A.-5
B.±5
C.±25
D.不存在

答案： A

11. 将体积分别为 $600cm^3$ 和 $129cm^3$ 的长方体铁块,熔成一个正方体铁块,那么这个正方体铁块的棱长是9cm.

答案： 9

12. 已知 $\sqrt[3]{1 - 3y}$ 与 $\sqrt[3]{4x - 1}$ 互为相反数(其中 $y ≠ 0$),则 $\frac{2x}{y} = $$\frac{3}{2}$.

答案： $\frac{3}{2}$ [点拨]由$\sqrt[3]{1 - 3y}$与$\sqrt[3]{4x - 1}$互为相反数，可得1 - 3y与4x - 1互为相反数，
∴$4x - 1 + 1 - 3y = 0$，解得$y=\frac{4}{3}x$。将$y=\frac{4}{3}x$代入$\frac{2x}{y}$，可得$\frac{2x}{y}=\frac{2x}{\frac{4}{3}x}=\frac{3}{2}$。

13. 下列四个实数中,不是无理数的是(C)
A.$\sqrt{2}$
B.$\pi$
C.$\frac{1}{3}$
D.5.855 855 58…

答案： C

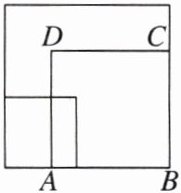
14. 大、中、小三个正方形按如图所示的方式摆放,若大正方形的面积为 5,小正方形的面积为 1,则正方形 $ABCD$ 的边长可能是(B)

A.1

B.$\sqrt{3}$
C.$\sqrt{5}$
D.3

答案： B

15. 绝对值为 $2 - \sqrt{3}$ 的数是$\sqrt{3}-2$或$2-\sqrt{3}$.

答案： $\sqrt{3}-2$或$2-\sqrt{3}$

16. 比较大小(填“＜”“=”或“＞”)：
(1) -$\sqrt{6}$＜$\sqrt{2}$；(2) $\sqrt[3]{7}$＜2.

答案：
(1)＜
(2)＜

17. 如图,数轴上点 $A$,$B$,$C$,$D$ 所对应的数分别是 1,2,3,4.若点 $E$ 对应的数是 $\sqrt{12}$,则点 $E$ 落在③之间(填序号).
① $A$ 和 $B$
② $B$ 和 $C$
③ $C$ 和 $D$
]

答案： ③