第85页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
14.(12 分)[2025 承德月考] 先化简,再求值:$ (1+\frac{2}{a-2}) ÷ \frac{a^{2}-4}{a^{2}-4a+4} $,其中 $ a= \sqrt{2}-2 $.
答案:
【解】原式=$\left( \frac{a-2}{a-2}+\frac{2}{a-2} \right) × \frac{(a-2)^2}{(a-2)(a+2)}=\frac{a}{a-2} × \frac{a-2}{a+2}=\frac{a}{a+2}$.当a=$\sqrt{2}$-2时,原式=$\frac{\sqrt{2}-2}{\sqrt{2}-2+2}=\frac{\sqrt{2}-2}{\sqrt{2}}=\frac{(\sqrt{2}-2) × \sqrt{2}}{\sqrt{2} × \sqrt{2}}=\frac{2-2\sqrt{2}}{2}=1-\sqrt{2}$.
15.(14 分)情境题 游戏活动型 淇淇玩一个摸球计算游戏,在一个密闭的容器中放入四个小球,小球分别标有如图所示的数. 现从容器中摸取小球,规定:若摸取到白色球,就加上球上的数:若摸到灰色球,就减去球上的数.

(1)若淇淇摸取到如下两个小球,请计算出结果.
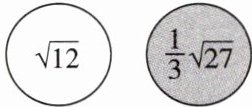
(2)若淇淇摸出全部的四个球,计算结果为 $ x $,嘉嘉说 $ x $ 的值与 $ \sqrt{48} $ 属于同类二次根式,你认为嘉嘉的说法对吗?并说明理由.

(1)若淇淇摸取到如下两个小球,请计算出结果.

(2)若淇淇摸出全部的四个球,计算结果为 $ x $,嘉嘉说 $ x $ 的值与 $ \sqrt{48} $ 属于同类二次根式,你认为嘉嘉的说法对吗?并说明理由.
答案:
【解】
(1)依题意,得$\sqrt{12}-\frac{1}{3}\sqrt{27}=2\sqrt{3}-\sqrt{3}=\sqrt{3}$.
(2)嘉嘉的说法对.理由如下:依题意,得$\sqrt{12}-\frac{1}{3}\sqrt{27}+\sqrt{6}-2\sqrt{\frac{3}{2}}=\sqrt{3}+\sqrt{6}-\sqrt{6}=\sqrt{3}$.
∵$\sqrt{48}=4\sqrt{3}$,与$\sqrt{3}$是同类二次根式,故嘉嘉的说法对.
(1)依题意,得$\sqrt{12}-\frac{1}{3}\sqrt{27}=2\sqrt{3}-\sqrt{3}=\sqrt{3}$.
(2)嘉嘉的说法对.理由如下:依题意,得$\sqrt{12}-\frac{1}{3}\sqrt{27}+\sqrt{6}-2\sqrt{\frac{3}{2}}=\sqrt{3}+\sqrt{6}-\sqrt{6}=\sqrt{3}$.
∵$\sqrt{48}=4\sqrt{3}$,与$\sqrt{3}$是同类二次根式,故嘉嘉的说法对.
16.(16 分)新考法 猜想验证法 如图,将边长分别为 $ 1,1+\sqrt{2},1+2\sqrt{2},1+3\sqrt{2} $ 的正方形的面积记为 $ S_{1},S_{2},S_{3},S_{4} $.
(1)计算:$ S_{2}-S_{1},S_{3}-S_{2},S_{4}-S_{3} $.
(2)把边长为 $ 1+(n-1)\sqrt{2} $ 的正方形的面积记作 $ S_{n} $,其中 $ n $ 是整数,从(1)中计算结果,你能猜出 $ S_{n+1}-S_{n} $ 等于多少吗?你的猜想是否正确,请说明理由.
(3)若将边长变为 $ a,a+\sqrt{b},a+2\sqrt{b},a+3\sqrt{b} $ 时,$ S_{n+1}-S_{n} $ 的值是多少?

(1)计算:$ S_{2}-S_{1},S_{3}-S_{2},S_{4}-S_{3} $.
(2)把边长为 $ 1+(n-1)\sqrt{2} $ 的正方形的面积记作 $ S_{n} $,其中 $ n $ 是整数,从(1)中计算结果,你能猜出 $ S_{n+1}-S_{n} $ 等于多少吗?你的猜想是否正确,请说明理由.
(3)若将边长变为 $ a,a+\sqrt{b},a+2\sqrt{b},a+3\sqrt{b} $ 时,$ S_{n+1}-S_{n} $ 的值是多少?

答案:
【解】
(1)$S_2 - S_1=(1+\sqrt{2})^2 - 1^2=1+2\sqrt{2}+2-1=2+2\sqrt{2}$;$S_3 - S_2=(1+2\sqrt{2})^2 - (1+\sqrt{2})^2=1+4\sqrt{2}+8-1-2\sqrt{2}-2=6+2\sqrt{2}$;$S_4 - S_3=(1+3\sqrt{2})^2 - (1+2\sqrt{2})^2=1+6\sqrt{2}+18-1-4\sqrt{2}-8=10+2\sqrt{2}$.
(2)$S_{n+1}-S_n=4n-2+2\sqrt{2}$.理由如下:$S_{n+1}-S_n=(1+n\sqrt{2})^2 - [1+(n-1)\sqrt{2}]^2=1+2\sqrt{2}n+2n^2 - [1+2\sqrt{2}(n-1)+2(n-1)^2]=1+2\sqrt{2}n+2n^2 - (1+2\sqrt{2}n-2\sqrt{2}+2n^2 - 4n+2)=1+2\sqrt{2}n+2n^2 -1-2\sqrt{2}n+2\sqrt{2}-2n^2 +4n-2=4n-2+2\sqrt{2}$.
(3)由题意得,$S_{n+1}-S_n=(a+n\sqrt{b})^2 - [a+(n-1)\sqrt{b}]^2=a^2 + 2an\sqrt{b} + n^2b - [a^2 + 2a(n-1)\sqrt{b} + (n-1)^2b]=a^2 + 2an\sqrt{b} + n^2b - (a^2 + 2an\sqrt{b} - 2a\sqrt{b} + n^2b - 2nb + b)=a^2 + 2an\sqrt{b} + n^2b - a^2 - 2an\sqrt{b} + 2a\sqrt{b} - n^2b + 2nb - b=2nb - b + 2a\sqrt{b}$.
(1)$S_2 - S_1=(1+\sqrt{2})^2 - 1^2=1+2\sqrt{2}+2-1=2+2\sqrt{2}$;$S_3 - S_2=(1+2\sqrt{2})^2 - (1+\sqrt{2})^2=1+4\sqrt{2}+8-1-2\sqrt{2}-2=6+2\sqrt{2}$;$S_4 - S_3=(1+3\sqrt{2})^2 - (1+2\sqrt{2})^2=1+6\sqrt{2}+18-1-4\sqrt{2}-8=10+2\sqrt{2}$.
(2)$S_{n+1}-S_n=4n-2+2\sqrt{2}$.理由如下:$S_{n+1}-S_n=(1+n\sqrt{2})^2 - [1+(n-1)\sqrt{2}]^2=1+2\sqrt{2}n+2n^2 - [1+2\sqrt{2}(n-1)+2(n-1)^2]=1+2\sqrt{2}n+2n^2 - (1+2\sqrt{2}n-2\sqrt{2}+2n^2 - 4n+2)=1+2\sqrt{2}n+2n^2 -1-2\sqrt{2}n+2\sqrt{2}-2n^2 +4n-2=4n-2+2\sqrt{2}$.
(3)由题意得,$S_{n+1}-S_n=(a+n\sqrt{b})^2 - [a+(n-1)\sqrt{b}]^2=a^2 + 2an\sqrt{b} + n^2b - [a^2 + 2a(n-1)\sqrt{b} + (n-1)^2b]=a^2 + 2an\sqrt{b} + n^2b - (a^2 + 2an\sqrt{b} - 2a\sqrt{b} + n^2b - 2nb + b)=a^2 + 2an\sqrt{b} + n^2b - a^2 - 2an\sqrt{b} + 2a\sqrt{b} - n^2b + 2nb - b=2nb - b + 2a\sqrt{b}$.
查看更多完整答案,请扫码查看


