第113页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
10. 如图,$\triangle ABC$是等边三角形,点$P在\triangle ABC$内,$PA = 4$,将$\triangle PAB绕点A逆时针旋转得到\triangle P_{1}AC$,连接$P_{1}P$,则$P_{1}P$的长等于(
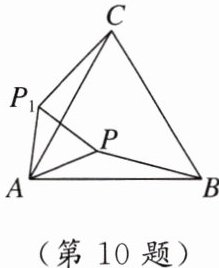
A.4
B.$2\sqrt{3}$
C.2
D.$\frac{3}{2}$
A
)
A.4
B.$2\sqrt{3}$
C.2
D.$\frac{3}{2}$
答案:
A
11. 如图,$\triangle ABC$中,$AC = DC = 3$,$BD垂直\angle BAC的平分线于D$,$E为AC$的中点,连接$BE交AD于点O$,则图中两个阴影三角形($\triangle OBD与\triangle OAE$)的面积之差的最大值为______。
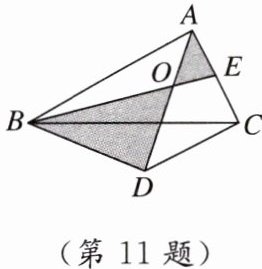

答案:
$\frac{9}{2}$ [点拨]如图,延长BD,AC交于点H.
∵AD⊥BH,
∴∠ADB=∠ADH=90°.
∴∠ABD+∠BAD=90°,∠H+∠HAD=90°.
∵AD平分∠BAC,
∴∠BAD=∠HAD.
∴∠ABD=∠H.
∴AB=AH.
∵AD⊥BH,
∴BD=DH.
∴$S_{\triangle ADB}=S_{\triangle ADH}$.
∵DC=CA,
∴∠CDA=∠CAD.
∵∠CAD+∠H=90°,∠CDA+∠CDH=90°,
∴∠CDH=∠H.
∴CH=CD=AC.
∴易得$S_{\triangle CDH}=\frac{1}{2}S_{\triangle ADH}=\frac{1}{4}S_{\triangle ABH}$.
∵E为AC的中点,
∴AE=EC=$\frac{1}{2}$AC.
∴易得$S_{\triangle ABE}=\frac{1}{4}S_{\triangle ABH}$.
∴$S_{\triangle ABE}=S_{\triangle CDH}$.
∵$S_{\triangle CED}-S_{\triangle AOE}=S_{\triangle ADB}-S_{\triangle ABE}=S_{\triangle ADH}-S_{\triangle CDH}=S_{\triangle ACD}$.
∵AC=CD=3,
∴当DC⊥AC 时,△ACD的面积最大,最大面积为$\frac{1}{2}$×3×3=$\frac{9}{2}$.故答案为$\frac{9}{2}$.
$\frac{9}{2}$ [点拨]如图,延长BD,AC交于点H.
∵AD⊥BH,
∴∠ADB=∠ADH=90°.
∴∠ABD+∠BAD=90°,∠H+∠HAD=90°.
∵AD平分∠BAC,
∴∠BAD=∠HAD.
∴∠ABD=∠H.
∴AB=AH.
∵AD⊥BH,
∴BD=DH.
∴$S_{\triangle ADB}=S_{\triangle ADH}$.
∵DC=CA,
∴∠CDA=∠CAD.
∵∠CAD+∠H=90°,∠CDA+∠CDH=90°,
∴∠CDH=∠H.
∴CH=CD=AC.
∴易得$S_{\triangle CDH}=\frac{1}{2}S_{\triangle ADH}=\frac{1}{4}S_{\triangle ABH}$.
∵E为AC的中点,
∴AE=EC=$\frac{1}{2}$AC.
∴易得$S_{\triangle ABE}=\frac{1}{4}S_{\triangle ABH}$.
∴$S_{\triangle ABE}=S_{\triangle CDH}$.
∵$S_{\triangle CED}-S_{\triangle AOE}=S_{\triangle ADB}-S_{\triangle ABE}=S_{\triangle ADH}-S_{\triangle CDH}=S_{\triangle ACD}$.
∵AC=CD=3,
∴当DC⊥AC 时,△ACD的面积最大,最大面积为$\frac{1}{2}$×3×3=$\frac{9}{2}$.故答案为$\frac{9}{2}$.

12. 如图,在$\triangle ABC$中,$AC = BC$,$\angle ACB = 100^{\circ}$,$D是AB$边上一点(不与$A$,$B$重合),以$CD为边作等腰三角形CDE$,$CD = CE$,且$\angle DCE = 100^{\circ}$,$CB与DE交于点F$,连接$BE$。
(1) 求证:$\triangle ACD\cong\triangle BCE$;
(2) 若$AD = BF$,求证:$\triangle DCF$是等腰三角形。
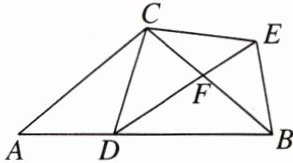
(1) 求证:$\triangle ACD\cong\triangle BCE$;
(2) 若$AD = BF$,求证:$\triangle DCF$是等腰三角形。

答案:
(1)[证明]
∵∠ACB=100°,∠DCE=100°,
∴∠ACB=∠DCE.
∴∠ACD=∠BCE.在△ACD和△BCE中,$\begin{cases} AC=BC, \\ ∠ACD=∠BCE, \\ CD=CE, \end{cases}$
∴△ACD≌△BCE(SAS).
(2)
∵AC=BC,∠ACB=100°,
∴∠A=∠CBA=$\frac{1}{2}$×(180°−100°)=40°.同理∠CDE=∠CED=40°.
∵△ACD≌△BCE,
∴AD=BE,∠A=∠CBE=40°.
∵AD=BF,
∴BE=BF.
∴∠BFE=∠BEF=$\frac{1}{2}$×(180°−40°)=70°,
∴∠DFC=∠BFE=70°.在△DCF中,∠CDE=40°,∠DFC=70°,
∴∠DCF=180°−40°−70°=70°=∠DFC.
∴△DCF是等腰三角形.
(1)[证明]
∵∠ACB=100°,∠DCE=100°,
∴∠ACB=∠DCE.
∴∠ACD=∠BCE.在△ACD和△BCE中,$\begin{cases} AC=BC, \\ ∠ACD=∠BCE, \\ CD=CE, \end{cases}$
∴△ACD≌△BCE(SAS).
(2)
∵AC=BC,∠ACB=100°,
∴∠A=∠CBA=$\frac{1}{2}$×(180°−100°)=40°.同理∠CDE=∠CED=40°.
∵△ACD≌△BCE,
∴AD=BE,∠A=∠CBE=40°.
∵AD=BF,
∴BE=BF.
∴∠BFE=∠BEF=$\frac{1}{2}$×(180°−40°)=70°,
∴∠DFC=∠BFE=70°.在△DCF中,∠CDE=40°,∠DFC=70°,
∴∠DCF=180°−40°−70°=70°=∠DFC.
∴△DCF是等腰三角形.
13. [2025沧州期末]已知在等边三角形$ABC$中,点$E在AB$上,点$D在CB$的延长线上,连接$ED$,$EC$,且$ED = EC$。
(1)【感知】如图①,当点$E为AB$的中点时,求证:$AE = DB$;
(2)【类比】如图②,当点$E为AB$边上任意一点时,则线段$AE与DB$的数量关系是______,嘉琪想到过点$E作\triangle ABC$其中一边的平行线构造出一个等边三角形,再利用全等三角形知识解决问题,填空并帮嘉琪完成证明;
(3)【拓展】如图③,在等边三角形$ABC$中,点$E在直线AB$上,点$D在线段CB$的延长线上,连接$ED$,$EC$,且$ED = EC$,若$\triangle ABC$的边长为1,$AE = 2$,直接写出$CD$的长。
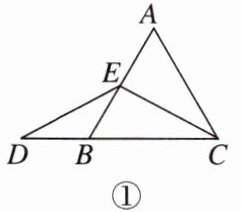
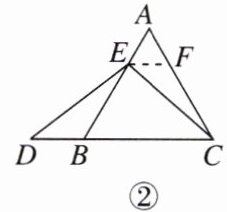
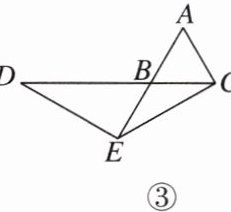
(1)【感知】如图①,当点$E为AB$的中点时,求证:$AE = DB$;
(2)【类比】如图②,当点$E为AB$边上任意一点时,则线段$AE与DB$的数量关系是______,嘉琪想到过点$E作\triangle ABC$其中一边的平行线构造出一个等边三角形,再利用全等三角形知识解决问题,填空并帮嘉琪完成证明;
(3)【拓展】如图③,在等边三角形$ABC$中,点$E在直线AB$上,点$D在线段CB$的延长线上,连接$ED$,$EC$,且$ED = EC$,若$\triangle ABC$的边长为1,$AE = 2$,直接写出$CD$的长。



答案:
(1)[证明]
∵ED=EC,
∴∠D=∠ECD.
∵△ABC是等边三角形,
∴∠ACB=∠ABC=60°.
∵点E为AB的中点,
∴AE=BE,∠ECD=$\frac{1}{2}$∠ACB=30°,
∴∠D=30°.
∵∠CBE=∠D+∠DEB=60°,
∴∠DEB=30°=∠D,
∴DB=BE.
∵AE=BE,
∴AE=BD.
(2)[解]AE=DB
证明:过点E作EF//BC,交AC于点F.
∵△ABC为等边三角形,
∴∠A=∠ABC=∠ACB=60°,AB=AC.
∵EF//BC,
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°.
∴△AEF为等边三角形.
∴AE=EF=AF.
∴AB−AE=AC−AF.
∴BE=CF.
∵ED=EC,
∴∠D=∠ECD.
∵∠DEB=∠ABC−∠D=60°−∠D,∠ECF=∠ACB−∠ECD=60°−∠ECD,
∴∠DEB=∠ECF.在△DBE和△EFC中,$\begin{cases} DE=EC, \\ ∠DEB=∠ECF, \\ BE=FC, \end{cases}$
∴△DBE≌△EFC(SAS).
∴DB=EF.
∴AE=DB.
(3)[解]CD=3. [点拨]如图所示,作EF//BC,交AC的延长线于点F,则∠DCE=∠CEF.易知∠ABC=60°,∠F=60°,△AEF是等边三角形.
∴AE=EF=2.
∵ED=EC,
∴∠D=∠DCE.
∴∠D=∠CEF.
∵∠DBE=∠ABC=60°,∠F=60°,
∴∠DBE=∠F.在△DBE和△EFC中,$\begin{cases} ∠DBE=∠F, \\ ∠D=∠CEF, \\ DE=EC, \end{cases}$
∴△DBE≌△EFC(AAS).
∴DB=EF=2.而BC=1,
∴CD=BC+DB=3.
(1)[证明]
∵ED=EC,
∴∠D=∠ECD.
∵△ABC是等边三角形,
∴∠ACB=∠ABC=60°.
∵点E为AB的中点,
∴AE=BE,∠ECD=$\frac{1}{2}$∠ACB=30°,
∴∠D=30°.
∵∠CBE=∠D+∠DEB=60°,
∴∠DEB=30°=∠D,
∴DB=BE.
∵AE=BE,
∴AE=BD.
(2)[解]AE=DB
证明:过点E作EF//BC,交AC于点F.
∵△ABC为等边三角形,
∴∠A=∠ABC=∠ACB=60°,AB=AC.
∵EF//BC,
∴∠AEF=∠ABC=60°,∠AFE=∠ACB=60°.
∴△AEF为等边三角形.
∴AE=EF=AF.
∴AB−AE=AC−AF.
∴BE=CF.
∵ED=EC,
∴∠D=∠ECD.
∵∠DEB=∠ABC−∠D=60°−∠D,∠ECF=∠ACB−∠ECD=60°−∠ECD,
∴∠DEB=∠ECF.在△DBE和△EFC中,$\begin{cases} DE=EC, \\ ∠DEB=∠ECF, \\ BE=FC, \end{cases}$
∴△DBE≌△EFC(SAS).
∴DB=EF.
∴AE=DB.
(3)[解]CD=3. [点拨]如图所示,作EF//BC,交AC的延长线于点F,则∠DCE=∠CEF.易知∠ABC=60°,∠F=60°,△AEF是等边三角形.
∴AE=EF=2.
∵ED=EC,
∴∠D=∠DCE.
∴∠D=∠CEF.
∵∠DBE=∠ABC=60°,∠F=60°,
∴∠DBE=∠F.在△DBE和△EFC中,$\begin{cases} ∠DBE=∠F, \\ ∠D=∠CEF, \\ DE=EC, \end{cases}$
∴△DBE≌△EFC(AAS).
∴DB=EF=2.而BC=1,
∴CD=BC+DB=3.

查看更多完整答案,请扫码查看


