第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. 下列二次根式中与$\sqrt{2}$是同类二次根式的是(
A.$\sqrt{24}$
B.$\sqrt{18}$
C.$\sqrt{12}$
D.$\sqrt{4}$
B
)A.$\sqrt{24}$
B.$\sqrt{18}$
C.$\sqrt{12}$
D.$\sqrt{4}$
答案:
B
2. 下列运算正确的是(
A.$\sqrt{a}+\sqrt{4a}= 3\sqrt{a}$
B.$\sqrt{8}-\sqrt{2}= \sqrt{6}$
C.$4+\sqrt{16}= 4\sqrt{16}$
D.$3\sqrt{2}-2\sqrt{2}= 1$
A
)A.$\sqrt{a}+\sqrt{4a}= 3\sqrt{a}$
B.$\sqrt{8}-\sqrt{2}= \sqrt{6}$
C.$4+\sqrt{16}= 4\sqrt{16}$
D.$3\sqrt{2}-2\sqrt{2}= 1$
答案:
A
3. [2025保定月考]若$\sqrt{12}与最简二次根式\sqrt{m - 1}$能合并,则$m$的值为(
A.1
B.2
C.3
D.4
D
)A.1
B.2
C.3
D.4
答案:
D
4. 若$m\sqrt{8}+\sqrt{32}-n\sqrt{2}= 5\sqrt{2}$,则下列结论正确的是(
A.$m = 0$,$n = 1$
B.$m = 1$,$n = 1$
C.$m = - 1$,$n = 0$
D.$m = 2$,$n = 4$
B
)A.$m = 0$,$n = 1$
B.$m = 1$,$n = 1$
C.$m = - 1$,$n = 0$
D.$m = 2$,$n = 4$
答案:
B
5. 新视角条件开放题将式子$\sqrt{35 - a}$($a$为正整数)化为最简二次根式后,可以与$\sqrt{8}$合并. 写出一个符合条件的$a$的值是
27(答案不唯一)
.
答案:
27(答案不唯一)
6. 二元一次方程组$\begin{cases}\sqrt{8}x-\sqrt{3}y = 7,\\\sqrt{2}x+\sqrt{3}y = - 1\end{cases} $的解是
$\left\{\begin{array}{l} x=\sqrt {2},\\ y=-\sqrt {3}\end{array}\right.$
.
答案:
$\left\{\begin{array}{l} x=\sqrt {2},\\ y=-\sqrt {3}\end{array}\right.$【点拨】$\left\{\begin{array}{l} \sqrt {8}x-\sqrt {3}y=7,①\\ \sqrt {2}x+\sqrt {3}y=-1,②\end{array}\right.$①+②,得$3\sqrt {2}x=6$,解得$x=\sqrt {2}$,将$x=\sqrt {2}$代入②,得$2+\sqrt {3}y=-1$,解得$y=-\sqrt {3}$.
∴方程组的解为$\left\{\begin{array}{l} x=\sqrt {2},\\ y=-\sqrt {3},\end{array}\right.$
∴方程组的解为$\left\{\begin{array}{l} x=\sqrt {2},\\ y=-\sqrt {3},\end{array}\right.$
7. 在长为$3\mathrm{dm}$,宽为$2\mathrm{dm}$的长方形木板中,采用如图的方式,在这块木板上

能
(填“能”或“不能”)截出$2个面积为2\mathrm{dm}^2$的正方形木板.
答案:
能
8. 母题教材P112习题T2计算:
(1) $\sqrt{125}+\frac{1}{4}\sqrt{3.2}-3\sqrt{0.2}$;
(2) $(\sqrt{20}+\sqrt{18})-(\sqrt{8}-\sqrt{125})$;
(3) $\sqrt{8x}-6\sqrt{\frac{x}{18}}+2x\sqrt{\frac{2}{x}}$.
(1) $\sqrt{125}+\frac{1}{4}\sqrt{3.2}-3\sqrt{0.2}$;
(2) $(\sqrt{20}+\sqrt{18})-(\sqrt{8}-\sqrt{125})$;
(3) $\sqrt{8x}-6\sqrt{\frac{x}{18}}+2x\sqrt{\frac{2}{x}}$.
答案:
【解】
(1)原式$=5\sqrt {5}+\frac {\sqrt {5}}{5}-\frac {3\sqrt {5}}{5}=\frac {23\sqrt {5}}{5}$.
(2)原式$=2\sqrt {5}+3\sqrt {2}-2\sqrt {2}+5\sqrt {5}=7\sqrt {5}+\sqrt {2}$.
(3)原式$=2\sqrt {2x}-\sqrt {2x}+2\sqrt {2x}=3\sqrt {2x}$.
(1)原式$=5\sqrt {5}+\frac {\sqrt {5}}{5}-\frac {3\sqrt {5}}{5}=\frac {23\sqrt {5}}{5}$.
(2)原式$=2\sqrt {5}+3\sqrt {2}-2\sqrt {2}+5\sqrt {5}=7\sqrt {5}+\sqrt {2}$.
(3)原式$=2\sqrt {2x}-\sqrt {2x}+2\sqrt {2x}=3\sqrt {2x}$.
9. 解方程:$2\sqrt{3}x= \sqrt{20}+\sqrt{48}x-\sqrt{\frac{1}{5}}$.
答案:
【解】$2\sqrt {3}x=\sqrt {20}+\sqrt {48}x-\sqrt {\frac {1}{5}}$,$2\sqrt {3}x=2\sqrt {5}+4\sqrt {3}x-\frac {\sqrt {5}}{5}$,$-2\sqrt {3}x=\frac {9\sqrt {5}}{5}$,$x=-\frac {3\sqrt {15}}{10}$.
10. 新考法数形结合法若$a+\sqrt{12}= \sqrt{27}$,则表示实数$a$的点会落在数轴的(
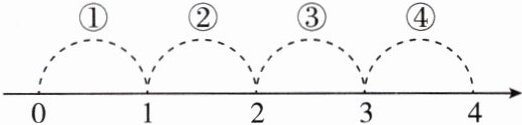
A.①段上
B.②段上
C.③段上
D.④段上
B
)
A.①段上
B.②段上
C.③段上
D.④段上
答案:
B【点拨】$\because a+\sqrt {12}=\sqrt {27}$,$\therefore a=\sqrt {27}-\sqrt {12}=3\sqrt {3}-2\sqrt {3}=\sqrt {3}$.又$\because \sqrt {1}<\sqrt {3}<\sqrt {4}$,$\therefore 1<\sqrt {3}<2$,即$1< a<2$,故表示实数$a$的点会落在数轴的②段上.故选 B.
11. [2025石家庄裕华区模拟]已知等腰三角形的两边长为$2\sqrt{3}和5\sqrt{2}$,则此等腰三角形的周长为(
A.$4\sqrt{3}+5\sqrt{2}$
B.$2\sqrt{3}+10\sqrt{2}$
C.$4\sqrt{3}+10\sqrt{2}$
D.$4\sqrt{3}+5\sqrt{2}或2\sqrt{3}+10\sqrt{2}$
B
)A.$4\sqrt{3}+5\sqrt{2}$
B.$2\sqrt{3}+10\sqrt{2}$
C.$4\sqrt{3}+10\sqrt{2}$
D.$4\sqrt{3}+5\sqrt{2}或2\sqrt{3}+10\sqrt{2}$
答案:
B【点拨】$\because 2×2\sqrt {3}<5\sqrt {2}$,$\therefore$只能是腰长为$5\sqrt {2}$.$\therefore$等腰三角形的周长$=2×5\sqrt {2}+2\sqrt {3}=10\sqrt {2}+2\sqrt {3}$.
12. 新考法新定义计算法我们规定运算符号“$\triangle$”的意义是:当$a > b$时,$a\triangle b = a + b$;当$a\leqslant b$时,$a\triangle b = a - b$,其他运算符号的意义不变,计算:$(\sqrt{3}\triangle\sqrt{2})-(2\sqrt{3}\triangle3\sqrt{2}) = $
$-\sqrt {3}+4\sqrt {2}$
.
答案:
$-\sqrt {3}+4\sqrt {2}$
查看更多完整答案,请扫码查看


