第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
15. 课堂上,老师出了一道题:比较 $\frac{\sqrt{19}-2},{3}$ 与 $\frac{2},{3}$ 的大小.
小荣的解法如下:
解:$\frac{\sqrt{19}-2},{3}-\frac{2},{3}= \frac{\sqrt{19}-2 - 2},{3}= \frac{\sqrt{19}-4},{3}$.
$\because 19>16,\therefore \sqrt{19}>4,\therefore \sqrt{19}-4>0$,
$\therefore \frac{\sqrt{19}-4},{3}>0,\therefore \frac{\sqrt{19}-2},{3}>\frac{2},{3}$.
我们把这种比较大小的方法称为作差法.
请利用上述方法比较实数 $\frac{\sqrt{94}-3},{9}$ 与 $\frac{2},{3}$ 的大小.
小荣的解法如下:
解:$\frac{\sqrt{19}-2},{3}-\frac{2},{3}= \frac{\sqrt{19}-2 - 2},{3}= \frac{\sqrt{19}-4},{3}$.
$\because 19>16,\therefore \sqrt{19}>4,\therefore \sqrt{19}-4>0$,
$\therefore \frac{\sqrt{19}-4},{3}>0,\therefore \frac{\sqrt{19}-2},{3}>\frac{2},{3}$.
我们把这种比较大小的方法称为作差法.
请利用上述方法比较实数 $\frac{\sqrt{94}-3},{9}$ 与 $\frac{2},{3}$ 的大小.
答案:
【解】√94-3/9-2/3=√94-3/9-6/9=√94-9/9.
∵94>81,
∴√94>9,
∴√94-9>0,
∴√94-9/9>0,
∴√94-3/9>2/3.
∵94>81,
∴√94>9,
∴√94-9>0,
∴√94-9/9>0,
∴√94-3/9>2/3.
16. 如图所示的是某数学兴趣小组的一次探究性活动.请你根据该小组的探究方法,探究下列问题:
已知 $9\pi$ 的整数部分为 $a,\sqrt[3]{28}$ 的小数部分为 $b$,求 $a + b$ 的值.

已知 $9\pi$ 的整数部分为 $a,\sqrt[3]{28}$ 的小数部分为 $b$,求 $a + b$ 的值.

答案:
【解】
∵9π≈9×3.14=28.26,
∴9π的整数部分是28,即a=28.
∵27<28<64,
∴³√27<³√28<³√64,即3<³√28<4.
∴³√28的整数部分是3.
∴³√28的小数部分是³√28-3,即b=³√28-3.
∴a+b=28+³√28-3=25+³√28.
∵9π≈9×3.14=28.26,
∴9π的整数部分是28,即a=28.
∵27<28<64,
∴³√27<³√28<³√64,即3<³√28<4.
∴³√28的整数部分是3.
∴³√28的小数部分是³√28-3,即b=³√28-3.
∴a+b=28+³√28-3=25+³√28.
17. 观察下列一组等式,解答后面的问题:
$(\sqrt{2}+1)(\sqrt{2}-1)= 1$,
$(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})= 1$,
$(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})= 1$,
$(\sqrt{5}+\sqrt{4})(\sqrt{5}-\sqrt{4})= 1$,
…
(1)观察上列各式计算,利用了
(2)根据上面的规律,计算下列式子的值:
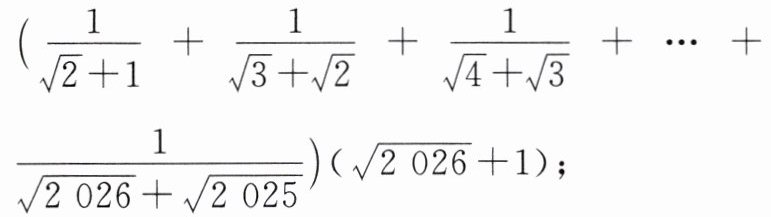
(3)利用上面的规律,比较 $\sqrt{2026}-\sqrt{2025}$ 与 $\sqrt{2027}-\sqrt{2026}$ 的大小.
$(\sqrt{2}+1)(\sqrt{2}-1)= 1$,
$(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})= 1$,
$(\sqrt{4}+\sqrt{3})(\sqrt{4}-\sqrt{3})= 1$,
$(\sqrt{5}+\sqrt{4})(\sqrt{5}-\sqrt{4})= 1$,
…
(1)观察上列各式计算,利用了
平方差
公式,小明想利用上面的规律使 $\frac{1},{\sqrt{n + 1}+\sqrt{n}}$ 的分母中不含根号,请你帮小明实现他的想法(写出过程);(2)根据上面的规律,计算下列式子的值:
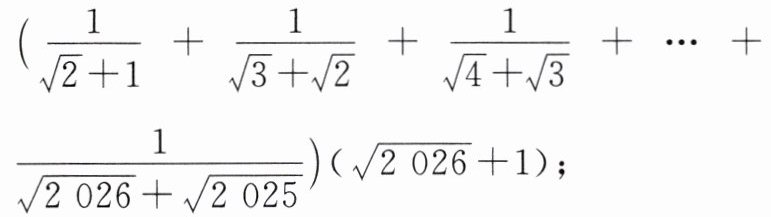
(3)利用上面的规律,比较 $\sqrt{2026}-\sqrt{2025}$ 与 $\sqrt{2027}-\sqrt{2026}$ 的大小.
答案:
【解】
(1)平方差 1/√n+1+√n=√n+1-√n/(√n+1+√n)(√n+1-√n)=√n+1-√n.
(2)(1/√2+1+1/√3+√2+1/√4+√3+…+1/√2026+√2025)(√2026+1)=(√2-1+√3-√2+√4-√3+…+√2026-√2025)(√2026+1)=(√2026-1)(√2026+1)=2026-1=2025.
(3)
∵√2026-√2025=(√2026-√2025)(√2026+√2025)/√2026+√2025=1/√2026+√2025,√2027-√2026=(√2027-√2026)(√2027+√2026)/√2027+√2026=1/√2027+√2026,√2026+√2025<√2027+√2026,
∴√2026-√2025>√2027-√2026.
(1)平方差 1/√n+1+√n=√n+1-√n/(√n+1+√n)(√n+1-√n)=√n+1-√n.
(2)(1/√2+1+1/√3+√2+1/√4+√3+…+1/√2026+√2025)(√2026+1)=(√2-1+√3-√2+√4-√3+…+√2026-√2025)(√2026+1)=(√2026-1)(√2026+1)=2026-1=2025.
(3)
∵√2026-√2025=(√2026-√2025)(√2026+√2025)/√2026+√2025=1/√2026+√2025,√2027-√2026=(√2027-√2026)(√2027+√2026)/√2027+√2026=1/√2027+√2026,√2026+√2025<√2027+√2026,
∴√2026-√2025>√2027-√2026.
查看更多完整答案,请扫码查看


