第102页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. 真实情境题 体育赛事 中国代表队在第 33 届巴黎奥运会中取得了 40 金 27 银 24 铜的傲人成绩,以下奥运比赛项目图标中,$\underline{不是}$中心对称图形的是 (
]

C
)]

答案:
C
2. 如图,$\triangle ABC与\triangle DEF关于点O$中心对称,则下列结论不一定正确的是 (
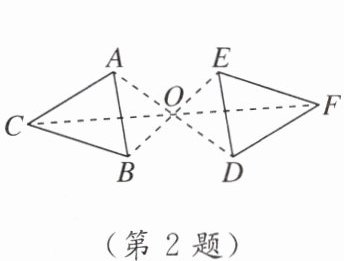
A.$BC = EF$
B.$\triangle ABC\cong\triangle DEF$
C.$OA = OB$
D.$AB// DE$
]
C
)
A.$BC = EF$
B.$\triangle ABC\cong\triangle DEF$
C.$OA = OB$
D.$AB// DE$
]
答案:
C
3. 如图,已知$\triangle ABC与\triangle DEF$成中心对称,则对称中心可能是 (

A.点$C$
B.点$E$
C.线段$BC$的中点
D.线段$BE$的中点
]
D
)
A.点$C$
B.点$E$
C.线段$BC$的中点
D.线段$BE$的中点
]
答案:
D
4. 下列四组图形中,右边图形与左边图形成中心对称的有$\underline{
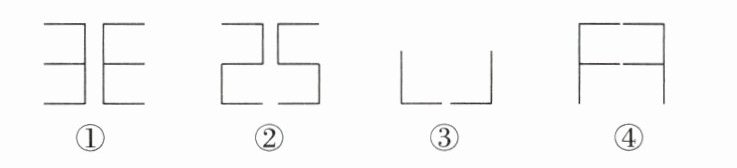
①
}$(填序号).
答案:
①
5. 如图是由边长为 1 的小等边三角形构成的网格,其中有 3 个小等边三角形已涂灰,把余下的白色小等边三角形中的一个涂灰,使图中的灰色部分构成一个中心对称图形,则满足条件的小等边三角形有$\underline{
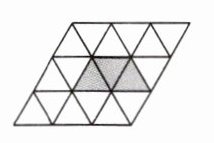
2
}$个.
答案:
2
6. 如图,在网格中,已知格点三角形$ABC和点O$,画出$\triangle ABC关于点O成中心对称的\triangle A'B'C'$(点$A$,$B$,$C的对应点分别为A'$,$B'$,$C'$).
]

]

答案:
【解】如图所示,△A'B'C'为所作.

【解】如图所示,△A'B'C'为所作.

7. 如图,在$4×4$的方格纸中,画格点三角形(顶点均在格点上)与$\triangle ABC$关于方格纸中的一个格点成中心对称,这样的三角形有 ( )

A.1 个
B.2 个
C.3 个
D.4 个
]

A.1 个
B.2 个
C.3 个
D.4 个
]
答案:
B 【点拨】如图所示,△A₁B₁C₁即为所求.

则这样的△A₁B₁C₁有2个.
B 【点拨】如图所示,△A₁B₁C₁即为所求.

则这样的△A₁B₁C₁有2个.
8. 如图,小明家的住房平面图呈长方形,被分割成 3 个正方形和 2 个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为 (

A.①②
B.②③
C.①③
D.①②③
]
①②
)
A.①②
B.②③
C.①③
D.①②③
]
答案:
A 【点拨】设图形①的长和宽分别是a,c,图形②的边长是b,图形③的边长是d,原长方形周长是l,则l=2(a+2b+c).
由题意可得$\left\{\begin{array}{l} a=b+d,\\ b=c+d,\end{array}\right. $
∴2b=a+c.
∴l=2(a+2b+c)=4(a+c)=8b.
∴2(a+c)=$\frac {l}{2}$,4b=$\frac {l}{2}$.
∵图形①的周长是2(a+c),图形②的周长是4b,
∴分割后不用测量就知道周长的图形标号为①②.
由题意可得$\left\{\begin{array}{l} a=b+d,\\ b=c+d,\end{array}\right. $
∴2b=a+c.
∴l=2(a+2b+c)=4(a+c)=8b.
∴2(a+c)=$\frac {l}{2}$,4b=$\frac {l}{2}$.
∵图形①的周长是2(a+c),图形②的周长是4b,
∴分割后不用测量就知道周长的图形标号为①②.
9. 如图,$\triangle ABC与\triangle DEC关于点C$成中心对称,$AG为\triangle ABC$的高,若$CE = 5$,$AG = 2$,则$S_{\triangle DEC}= \underline{
]

5
}$.]

答案:
5 【点拨】
∵△ABC与△DEC关于点C成中心对称,
∴CE=BC=5,$S_{\triangle DEC}=S_{\triangle ABC}$,
∴$S_{\triangle ABC}=\frac {1}{2}BC× AG=\frac {1}{2}×5×2=5$,
∴$S_{\triangle DEC}=5$.
∵△ABC与△DEC关于点C成中心对称,
∴CE=BC=5,$S_{\triangle DEC}=S_{\triangle ABC}$,
∴$S_{\triangle ABC}=\frac {1}{2}BC× AG=\frac {1}{2}×5×2=5$,
∴$S_{\triangle DEC}=5$.
10. 如图①所示,魔术师把 4 张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把其中 1 张扑克牌旋转$180^{\circ}$.魔术师睁开眼睛后,看到 4 张扑克牌如图②所示,则被旋转的扑克牌上的数字是
]
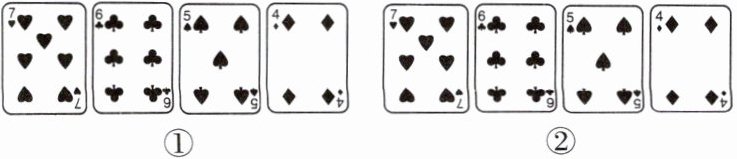
4
.]

答案:
4 【点拨】数字为7,6,5的扑克牌上的图形都不能找到这样的一个点,使牌面上的图形绕该点旋转180°后与原来的图形重合,数字为4的扑克牌绕某一点旋转180°后牌面上的图形能够与原来的图形重合,所以被旋转的扑克牌上的数字是4.
查看更多完整答案,请扫码查看


