《2025年综合应用创新题典中点八年级数学上册冀教版》

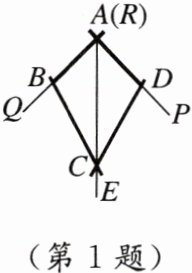
1. 如图,小敏做了一个角平分仪$ABCD$,其中$AB = AD$,$BC = DC$,将仪器上的点$A与∠PRQ的顶点R$重合,调整$AB和AD$,使它们分别落在角的两边上,过点$A$,$C画一条射线AE$,$AE就是∠PRQ$的平分线. 此角平分仪的画图原理是(A)

A.SSS
B.SAS
C.ASA
D.AAS
]

答案： A

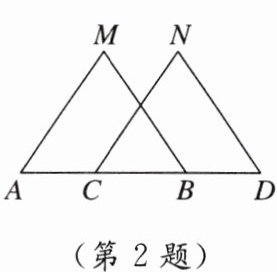
2. 如图,已知$MB = ND$,$∠MBA = ∠NDC$,下列哪一个选项不能用于判定$△ABM≌△CDN$的是(C)

A.$∠M = ∠N$
B.$AB = CD$
C.$AM = CN$
D.$AM// CN$
]

答案： C

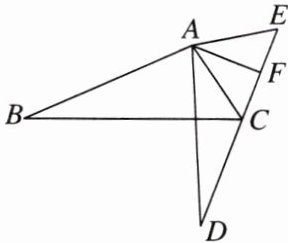
3. 如图,$∠BAD = ∠CAE$,$AB = AD$,$AC = AE$,且$E$,$C$,$D$在同一直线上.
(1) 填空：观察可知,将$△ABC$绕点A逆时针旋转,可与$△$______ADE重合；
(2) 求证：$BC = DE$；
(3) 若$∠B = 30^{\circ}$,$∠BAC = 100^{\circ}$,点$F是CE$的中点,连接$AF$,则$∠FAE$的度数为40°.
]

答案：
(1)A;ADE
(2)[证明]
∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,即∠BAC=∠DAE.
在△ABC和△ADE中，{AB=AD,∠BAC=∠DAE,AC=AE}
∴△ABC≌△ADE(SAS),
∴BC=DE.
(3)40°　[点拨]
∵点F是CE的中点，
∴CF=EF.
在△ACF和△AEF中,{AF=AF,AC=AE,CF=EF}
∴△ACF≌△AEF(SSS),
∴∠AFC=∠AFE=$\frac{1}{2}$∠CFE=$\frac{1}{2}$×180°=90°.
∵∠B+∠ACB+∠BAC=180°,∠B=30°,∠BAC=100°,
∴∠ACB=180°−∠B−∠BAC=50°.
由
(2)可知△ABC≌△ADE,
∴∠E=∠ACB=50°,
∴∠FAE=90°−∠E=40°.

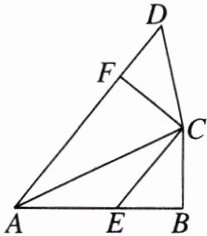
4. 如图,在四边形$ABCD$中,$E$,$F分别是边AB$,$AD$上一点,$CD = CE$,$∠BEC = ∠D$,$∠B + ∠AFC = 180^{\circ}$.
(1) 求证：$EB = DF$；
(2) 连接$AC$,若$CA平分∠BCF$. 求证：$AB = AF$.
]

答案：
(1)[证明]
∵∠B+∠AFC=180°,∠DFC+∠AFC=180°,
∴∠B=∠DFC.
在△BCE和△FCD中,{∠B=∠DFC,∠BEC=∠D,CE=CD}
∴△BCE≌△FCD(AAS),
∴EB=DF.
(2)[证明]由
(1)知△BCE≌△FCD,
∴BC=FC.
∵CA平分∠BCF,
∴∠BCA=∠FCA.
在△ABC和△AFC中，{BC=FC,∠BCA=∠FCA,AC=AC}
∴△ABC≌△AFC(SAS),
∴AB=AF.

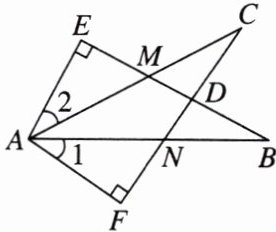
5. 如图,$EB交AC于点M$,交$FC于点D$,$AB交FC于点N$,$∠E = ∠F = 90^{\circ}$,$∠B = ∠C$,$AE = AF$,给出下列结论,其中正确的结论有(C)
①$∠1 = ∠2$；
②$BE = CF$；
③$△ACN≌△ABM$；
④$CD = DN$；
⑤$△AFN≌△AEM$.

A.2个
B.3个
C.4个
D.5个
]

答案： C　[点拨]
∵∠E=∠F=90°,∠B=∠C,AE=AF,
∴△ABE≌△ACF(AAS),
∴BE=CF,∠BAE=∠CAF,故②正确.
∵∠BAE=∠CAF,
∴∠BAE−∠BAC=∠CAF−∠BAC,即∠1=∠2,故①正确.
∵△ABE≌△ACF,
∴AB=AC.又
∵∠BAC=∠CAB,∠B=∠C,
∴△ACN≌△ABM(ASA),故③正确.CD=DN不能证明成立，故④错误.
∵∠1=∠2,∠F=∠E,AF=AE,
∴△AFN≌△AEM(ASA),故⑤正确,故选C.

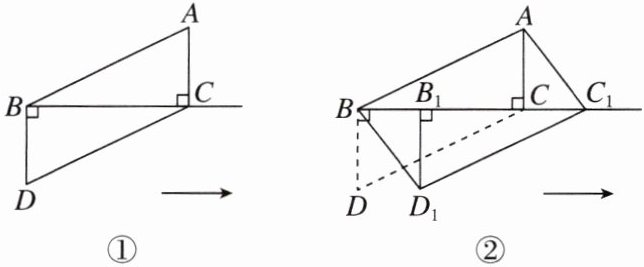
6. [2025 北京东城区校级模拟] 如图①,$△ABC与△DCB$全等,且$∠ACB = ∠DBC = 90^{\circ}$,$BC = 6$. 如图②,将$△DBC沿射线BC方向平移得到△D_{1}B_{1}C_{1}$,连接$AC_{1}$,$BD_{1}$.
(1) 求证：$BD_{1} = AC_{1}且BD_{1}// AC_{1}$；
(2)6 $△DBC沿射线BC$方向平移的距离等于______时,点$A与点D_{1}$之间的距离最小.
]

答案：
(1)[证明]由题图①可知,△ABC≌△DCB,
∴AC=BD.
由平移的性质可知BD=B₁D₁,∠DBC=∠D₁B₁C₁=90°,BB₁=CC₁,
∴AC=B₁D₁,∠BB₁D₁=90°.
∵∠ACB=90°,
∴∠ACC₁=90°.
在△BB₁D₁和△C₁CA中,{B₁D₁=AC,∠BB₁D₁=∠ACC₁=90°,BB₁=CC₁}
∴△BB₁D₁≌△C₁CA(SAS).
∴∠AC₁C=∠D₁BB₁,BD₁=AC₁,
∴BD₁//AC₁.
∴BD₁=AC₁且BD₁//AC₁.
(2)6