第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. [2025石家庄新华区月考]化简$\frac{3m + n}{m - n} - \frac{4n}{m - n}$的结果是(
A.1
B.-1
C.$\frac{m - 5n}{m - n}$
D.3
D
)A.1
B.-1
C.$\frac{m - 5n}{m - n}$
D.3
答案:
D
2. 新考法 数形结合法 若x是非负整数,则表示$\frac{2x}{x + 2} - \frac{x^2 - 4}{(x + 2)^2}$的值的对应点落在如图所示的数轴上的范围是(
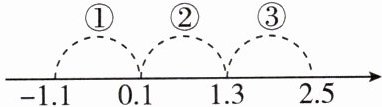
A.①
B.②
C.③
D.①或②
B
)
A.①
B.②
C.③
D.①或②
答案:
B 【点拨】原式$=\frac{2x}{x+2}-\frac{(x+2)(x-2)}{(x+2)^2}=\frac{2x}{x+2}-\frac{x-2}{x+2}=$$\frac{2x-(x-2)}{x+2}=\frac{2x-x+2}{x+2}=\frac{x+2}{x+2}=1$,则表示$\frac{2x}{x+2}-$$\frac{x^2-4}{(x+2)^2}$的值的对应点落在数轴上的范围是②.
3. [2024河北]已知A为整式,若计算$\frac{A}{xy + y^2} - \frac{y}{x^2 + xy}的结果为\frac{x - y}{xy}$,则A = (
A.x
B.y
C.x + y
D.x - y
A
)A.x
B.y
C.x + y
D.x - y
答案:
A
4. 新考法 整体代入法 若a,b互为倒数,且a ≠ b,则分式$\frac{a^2b}{a - b} - \frac{ab^2}{a - b}$的值为
1
。
答案:
1
5. 分式$\frac{1}{x^2 - 2x}与\frac{2}{x^2 - 4}$的最简公分母是
$x(x+2)(x-2)$
。
答案:
$x(x+2)(x-2)$【点拨】分式$\frac{1}{x^2-2x}$与$\frac{2}{x^2-4}$的分母分别是$x^2-2x=x(x-2)$,$x^2-4=(x+2)(x-2)$,故最简公分母是$x(x+2)(x-2)$.
6. 若将分式$\frac{3x^2}{x^2 - y^2}与分式\frac{x}{2(x - y)}$通分后,分式$\frac{x}{2(x - y)}$的分母变为2(x + y)(x - y),则分式$\frac{3x^2}{x^2 - y^2}$的分子应变为
$6x^2$
。
答案:
$6x^2$
7. 计算:
(1)$\frac{3a - 2}{a^2 - a} + \frac{2a - 1}{a - a^2}$;
(2)$\frac{x^2}{x + 3} - x + 3$;
(3)$\frac{a^2 - 4}{a^2 - 4a + 4} - \frac{1}{a - 2} - \frac{a}{a + 2}$。
(1)$\frac{3a - 2}{a^2 - a} + \frac{2a - 1}{a - a^2}$;
(2)$\frac{x^2}{x + 3} - x + 3$;
(3)$\frac{a^2 - 4}{a^2 - 4a + 4} - \frac{1}{a - 2} - \frac{a}{a + 2}$。
答案:
【解】
(1)原式$=\frac{3a-2}{a^2-a}-\frac{2a-1}{a^2-a}=\frac{3a-2-(2a-1)}{a^2-a}=$$\frac{3a-2-2a+1}{a(a-1)}=\frac{a-1}{a(a-1)}=\frac{1}{a}$.
(2)原式$=\frac{x^2}{x+3}-\frac{x-3}{1}=\frac{x^2}{x+3}-\frac{x^2-9}{x+3}=\frac{9}{x+3}$.
(3)原式$=\frac{(a-2)(a+2)}{(a-2)^2}-\frac{1}{a-2}-\frac{a}{a+2}$$=\frac{a+2}{a-2}-\frac{1}{a-2}-\frac{a}{a+2}=\frac{a+1}{a-2}-\frac{a}{a+2}$$=\frac{(a+1)(a+2)-a(a-2)}{(a-2)(a+2)}=\frac{a^2+3a+2-a^2+2a}{a^2-4}$$=\frac{5a+2}{a^2-4}$.
(1)原式$=\frac{3a-2}{a^2-a}-\frac{2a-1}{a^2-a}=\frac{3a-2-(2a-1)}{a^2-a}=$$\frac{3a-2-2a+1}{a(a-1)}=\frac{a-1}{a(a-1)}=\frac{1}{a}$.
(2)原式$=\frac{x^2}{x+3}-\frac{x-3}{1}=\frac{x^2}{x+3}-\frac{x^2-9}{x+3}=\frac{9}{x+3}$.
(3)原式$=\frac{(a-2)(a+2)}{(a-2)^2}-\frac{1}{a-2}-\frac{a}{a+2}$$=\frac{a+2}{a-2}-\frac{1}{a-2}-\frac{a}{a+2}=\frac{a+1}{a-2}-\frac{a}{a+2}$$=\frac{(a+1)(a+2)-a(a-2)}{(a-2)(a+2)}=\frac{a^2+3a+2-a^2+2a}{a^2-4}$$=\frac{5a+2}{a^2-4}$.
8. 新考法 作差比较法 已知$P = \frac{a^2 + b^2}{a^2 - b^2}$,$Q = \frac{2ab}{a^2 - b^2}$,其中a > b > 0,则P,Q的大小关系是(
A.P = Q
B.P > Q
C.P < Q
D.不能确定
B
)A.P = Q
B.P > Q
C.P < Q
D.不能确定
答案:
B
9. [2024雅安]已知$\frac{2}{a} + \frac{1}{b} = 1$(a + b ≠ 0),则$\frac{a + ab}{a + b} = $(
A.$\frac{1}{2}$
B.1
C.2
D.3
2
)A.$\frac{1}{2}$
B.1
C.2
D.3
答案:
C 【点拨】$\because\frac{2}{a}+\frac{1}{b}=1(a+b\neq0)$,$\therefore\frac{2b+a}{ab}=1$.$\therefore a+$$2b=ab$.$\therefore\frac{a+ab}{a+b}=\frac{a+a+2b}{a+b}=\frac{2(a+b)}{a+b}=2$,故选 C.
10. 新趋势 跨学科综合 照相机成像原理用公式$\frac{1}{f} = \frac{1}{u} + \frac{1}{v}$(v ≠ f)表示,其中f表示照相机镜头的焦距,u表示物体到镜头的距离,v表示胶片(像)到镜头的距离。已知f,v,则u = (
A.$\frac{fv}{f - v}$
B.$\frac{f - v}{fv}$
C.$\frac{fv}{v - f}$
D.$\frac{v - f}{fv}$
C
)A.$\frac{fv}{f - v}$
B.$\frac{f - v}{fv}$
C.$\frac{fv}{v - f}$
D.$\frac{v - f}{fv}$
答案:
C
11. 新考法 整体求值法 已知实数x,y,z满足$\frac{1}{x + y} + \frac{1}{y + z} + \frac{1}{z + x} = \frac{7}{6}$,且$\frac{z}{x + y} + \frac{x}{y + z} + \frac{y}{z + x} = 11$,则x + y + z的值为(
A.12
B.14
C.$\frac{22}{7}$
D.9
12
)A.12
B.14
C.$\frac{22}{7}$
D.9
答案:
A 【点拨】$\because\frac{x}{x+y}+\frac{x}{y+z}+\frac{y}{z+x}=11$,$\therefore1+\frac{z}{x+y}+1+\frac{x}{y+z}+1+\frac{y}{z+x}=14$,即$\frac{x+y+z}{x+y}+\frac{x+y+z}{y+z}+\frac{x+y+z}{z+x}=14$.$\therefore\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}=\frac{14}{x+y+z}$.又$\because\frac{1}{x+y}+\frac{1}{y+z}+\frac{1}{z+x}=\frac{7}{6}$,$\therefore\frac{14}{x+y+z}=\frac{7}{6}$.$\therefore x+y+z=12$.
查看更多完整答案,请扫码查看


