第100页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
1. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性. 下列汉字是轴对称图形的是(

A.遇
B.见
C.美
D.好
C
)
A.遇
B.见
C.美
D.好
答案:
C
2. 如图,AD 与 BC 交于点 O,△ABO 和△CDO 关于直线 PQ 对称,点 A,B 的对称点分别是点 C,D. 下列不一定正确的是(
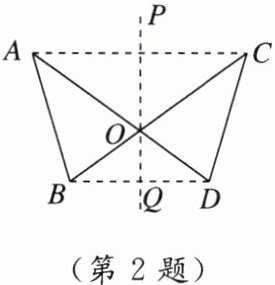
A.$ AD \perp BC $
B.$ AC \perp PQ $
C.$ \triangle ABO \cong \triangle CDO $
D.$ AC // BD $
A
)
A.$ AD \perp BC $
B.$ AC \perp PQ $
C.$ \triangle ABO \cong \triangle CDO $
D.$ AC // BD $
答案:
A
3. 在正方形网格中,$ \angle ACB $ 的位置如图所示,到 $ \angle ACB $ 两边距离相等的点是(
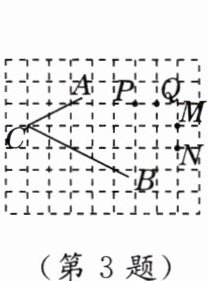
A.点 M
B.点 N
C.点 P
D.点 Q
A
)
A.点 M
B.点 N
C.点 P
D.点 Q
答案:
A
4. $ \triangle ABC $ 是一个任意三角形,用直尺和圆规作出 $ \angle A $,$ \angle B $ 的平分线,如果两条平分线交于点 O,那么下列说法中不正确的是(
A.点 O 一定在 $ \triangle ABC $ 的内部
B.$ \angle C $ 的平分线一定经过点 O
C.点 O 到 $ \triangle ABC $ 三边的距离一定相等
D.点 O 到 $ \triangle ABC $ 三个顶点的距离一定相等
D
)A.点 O 一定在 $ \triangle ABC $ 的内部
B.$ \angle C $ 的平分线一定经过点 O
C.点 O 到 $ \triangle ABC $ 三边的距离一定相等
D.点 O 到 $ \triangle ABC $ 三个顶点的距离一定相等
答案:
D
5. 如图,是由四个全等的直角三角形拼成的“赵爽弦图”,得到正方形 ABCD 与正方形 EFGH,连接 DF. 若 $ EF = \frac{1}{2}BG $,$ DF = 2\sqrt{3} $,则正方形 ABCD 的面积为(
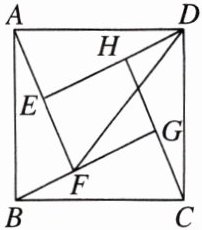
A.16
B.9
C.8
D.12
D
)
A.16
B.9
C.8
D.12
答案:
D 【点拨】由题意得,BG=AF,
∵EF= $\frac{1}{2}$BG,
∴EF= $\frac{1}{2}$AF. 又
∵DE⊥AF,
∴DE垂直平分线段AF,
∴DF=AD=2$\sqrt{3}$,
∴$S_{正方形ABCD}$=(2$\sqrt{3}$)²=12,故选 D.
∵EF= $\frac{1}{2}$BG,
∴EF= $\frac{1}{2}$AF. 又
∵DE⊥AF,
∴DE垂直平分线段AF,
∴DF=AD=2$\sqrt{3}$,
∴$S_{正方形ABCD}$=(2$\sqrt{3}$)²=12,故选 D.
6. 如图,$ AD // BC $,$ \angle ABC $ 的平分线 BP 与 $ \angle BAD $ 的平分线 AP 相交于点 P,作 $ PE \perp AB $ 于点 E. 若 $ PE = 2 $,则两平行线 AD 与 BC 间的距离为( )
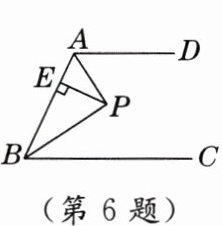
A.1
B.2
C.3
D.4

A.1
B.2
C.3
D.4
答案:
D 【点拨】如图,过点 P 作 PF⊥AD 于点 F,延长 FP 交 BC 于点 G.
∵∠BAD 的平分线是 AP,PE⊥AB,PF⊥AD,
∴PF=PE=2,∠AFG=90°.
∵AD//BC,
∴∠AFG+∠BGF=180°.
∴∠BGF=180°-90°=90°.
∴PG⊥BC.
∵∠ABC 的平分线是 BP,PE⊥AB,PG⊥BC,
∴PG=PE=2,
∴FG=PF+PG=2+2=4.
∴两平行线 AD 与 BC 间的距离为 4.
D 【点拨】如图,过点 P 作 PF⊥AD 于点 F,延长 FP 交 BC 于点 G.
∵∠BAD 的平分线是 AP,PE⊥AB,PF⊥AD,
∴PF=PE=2,∠AFG=90°.
∵AD//BC,
∴∠AFG+∠BGF=180°.
∴∠BGF=180°-90°=90°.
∴PG⊥BC.
∵∠ABC 的平分线是 BP,PE⊥AB,PG⊥BC,
∴PG=PE=2,
∴FG=PF+PG=2+2=4.
∴两平行线 AD 与 BC 间的距离为 4.

7. 如图,在 $ Rt \triangle ABC $ 中,$ \angle C = 90^{\circ} $,利用尺规在 BC,BA 上分别截取 BE,BD,使 $ BE = BD $;分别以 D,E 为圆心,以大于 $ \frac{1}{2}DE $ 的长为半径作弧,两弧在 $ \angle CBA $ 内交于点 F;作射线 BF 交 AC 于点 G. 若 $ CG = 1 $,P 为 AB 上一动点,则 GP 的最小值为( )
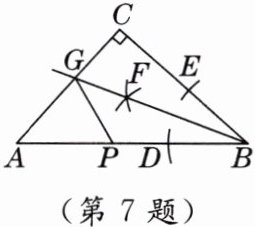
A.2
B.$ \frac{1}{2} $
C.1
D.无法确定

A.2
B.$ \frac{1}{2} $
C.1
D.无法确定
答案:
C 【点拨】如图,过点 G 作 GH⊥AB 于点 H.由题意可知,BG 平分∠ABC.又
∵GH⊥BA,∠C=90°,
∴GH=GC=1.根据垂线段最短可知,GP 的最小值为 1.
C 【点拨】如图,过点 G 作 GH⊥AB 于点 H.由题意可知,BG 平分∠ABC.又
∵GH⊥BA,∠C=90°,
∴GH=GC=1.根据垂线段最短可知,GP 的最小值为 1.

8. 如图,线段 AB,DE 的垂直平分线交于点 C,且 $ \angle ABC = \angle EDC = 78^{\circ} $,$ \angle AEB = 98^{\circ} $,则 $ \angle EBD $ 的度数为(
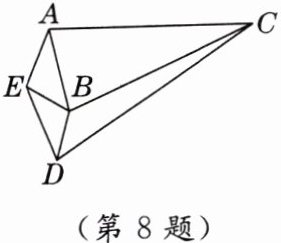
A.$ 162^{\circ} $
B.$ 152^{\circ} $
C.$ 122^{\circ} $
D.$ 112^{\circ} $
C
)
A.$ 162^{\circ} $
B.$ 152^{\circ} $
C.$ 122^{\circ} $
D.$ 112^{\circ} $
答案:
C 【点拨】连接 CE.
∵线段 AB,DE 的垂直平分线交于点 C,
∴CA=CB,CD=CE.易证得∠BAC=∠ABC=78°,∠DEC=∠EDC=78°,
∴∠ACB=∠DCE.
∴∠ACB-∠ECB=∠DCE-∠ECB,即∠ACE=∠BCD.在△BCD 和△ACE 中,$\begin{cases} CB=CA, \\ ∠BCD=∠ACE, \\ CD=CE, \end{cases}$
∴△BCD≌△ACE(SAS).
∴∠CBD=∠CAE=78°+∠BAE.
∵∠AEB=98°,
∴∠ABE=180°-∠AEB-∠BAE=180°-98°-∠BAE=82°-∠BAE.
∴∠EBD=360°-∠CBD-∠ABC-∠ABE=360°-(78°+∠BAE)-78°-(82°-∠BAE)=122°.
∵线段 AB,DE 的垂直平分线交于点 C,
∴CA=CB,CD=CE.易证得∠BAC=∠ABC=78°,∠DEC=∠EDC=78°,
∴∠ACB=∠DCE.
∴∠ACB-∠ECB=∠DCE-∠ECB,即∠ACE=∠BCD.在△BCD 和△ACE 中,$\begin{cases} CB=CA, \\ ∠BCD=∠ACE, \\ CD=CE, \end{cases}$
∴△BCD≌△ACE(SAS).
∴∠CBD=∠CAE=78°+∠BAE.
∵∠AEB=98°,
∴∠ABE=180°-∠AEB-∠BAE=180°-98°-∠BAE=82°-∠BAE.
∴∠EBD=360°-∠CBD-∠ABC-∠ABE=360°-(78°+∠BAE)-78°-(82°-∠BAE)=122°.
9. 如图,$ DE \perp AB $ 于点 E,$ DF \perp BC $ 于点 F,且 $ DE = DF $,若 $ \angle DBC = 50^{\circ} $,则 $ \angle ABC = $
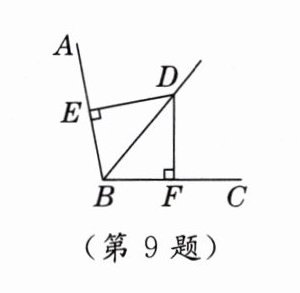
100
$ ^{\circ} $.
答案:
100
10. 如图,在锐角三角形 ABC 中,$ \angle A = 80^{\circ} $,DE 和 DF 分别垂直平分边 AB,AC,则 $ \angle DBC $ 的度数为 ______ $ ^{\circ} $.
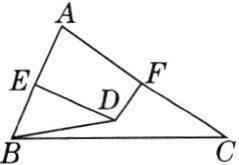

答案:
10 【点拨】如图,连接 DA,DC.
∵∠BAC=80°,
∴∠ABC+∠ACB=180°-80°=100°.
∵DE 和 DF 分别垂直平分边 AB,AC,
∴DA=DB,DA=DC.
∴DB=DC.易证得∠DBA=∠DAB,∠DAC=∠DCA,∠DBC=∠DCB,
∴∠DBA+∠DCA=∠DAB+∠DAC=80°.
∴∠DBC= $\frac{1}{2}$×(100°-80°)=10°.
10 【点拨】如图,连接 DA,DC.
∵∠BAC=80°,
∴∠ABC+∠ACB=180°-80°=100°.
∵DE 和 DF 分别垂直平分边 AB,AC,
∴DA=DB,DA=DC.
∴DB=DC.易证得∠DBA=∠DAB,∠DAC=∠DCA,∠DBC=∠DCB,
∴∠DBA+∠DCA=∠DAB+∠DAC=80°.
∴∠DBC= $\frac{1}{2}$×(100°-80°)=10°.

查看更多完整答案,请扫码查看


