第112页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
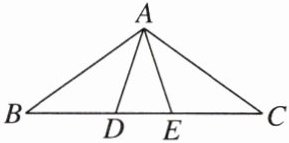
1. 如图,$\angle B= \angle C= 36^{\circ}$,$\angle ADE= \angle AED= 72^{\circ}$,则图中的等腰三角形有(
A.3个
B.4个
C.5个
D.6个
D
)
A.3个
B.4个
C.5个
D.6个
答案:
D
2. 如图,$\triangle ABC$中,$BO平分\angle ABC$,$CO平分\angle ACB$,$MN经过点O$,与$AB$,$AC相交于点M$,$N$,且$MN// BC$,已知$AB = 3$,$AC = 4$,则$\triangle AMN$的周长为(

A.6
B.7
C.8
D.9
B
)
A.6
B.7
C.8
D.9
答案:
B
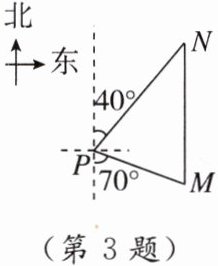
3. 如图,一艘海轮位于灯塔$P的南偏东70^{\circ}方向的M$处,它以每小时40海里的速度向正北方向航行,2小时后到达位于灯塔$P的北偏东40^{\circ}方向的N$处,则$N处与灯塔P$相距(
A.40海里
B.60海里
C.70海里
D.80海里
D
)
A.40海里
B.60海里
C.70海里
D.80海里
答案:
D
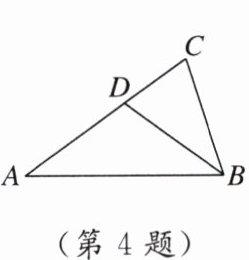
4. [2024重庆]如图,在$\triangle ABC$中,$AB = AC$,$\angle A = 36^{\circ}$,$BD平分\angle ABC交AC于点D$。若$BC = 2$,则$AD$的长度为______。

2
答案:
2
5. 如图,$\triangle ABC$是等边三角形,$D$,$E$,$F分别是AB$,$BC$,$CA$边上一点,且$AD = BE = CF$,则$\triangle DEF$

是
等边三角形(填“是”或“不是”)。
答案:
是
6. 如图,六边形$ABCDEF的六个角都是120^{\circ}$,边长$AB = 1\mathrm{cm}$,$BC = 3\mathrm{cm}$,$CD = 3\mathrm{cm}$,$DE = 2\mathrm{cm}$,则这个六边形的周长是______$\mathrm{cm}$。


答案:
15 [点拨]如图,分别作AB,CD,EF的延长线和反向延长线,使它们交于点G,H,P.
∵六边形ABCDEF的六个角都是120°,
∴它的每一个外角都是60°.
∴易得△APF,△BGC,△EDH,△PGH都是等边三角形.
∴GB=GC=BC=3cm,EH=DH=DE=2cm.
∴PG=PH=GH=3+3+2=8(cm).
∴FA=PF=PA=8−3−1=4(cm).
∴EF=8−4−2=2(cm).
∴六边形ABCDEF的周长为1+4+2+2+3+3=15(cm).
15 [点拨]如图,分别作AB,CD,EF的延长线和反向延长线,使它们交于点G,H,P.
∵六边形ABCDEF的六个角都是120°,
∴它的每一个外角都是60°.
∴易得△APF,△BGC,△EDH,△PGH都是等边三角形.
∴GB=GC=BC=3cm,EH=DH=DE=2cm.
∴PG=PH=GH=3+3+2=8(cm).
∴FA=PF=PA=8−3−1=4(cm).
∴EF=8−4−2=2(cm).
∴六边形ABCDEF的周长为1+4+2+2+3+3=15(cm).

7. 如图,将一张长方形的纸条$ABCD沿EF$折叠,点$D$,$C分别落在D'$,$C'$的位置上,$AD交EC'于点G$,若折叠后$\angle AGC' = 48^{\circ}$。
(1) 求$\angle CEF$的度数;
(2) 求证:$\triangle EFG$是等腰三角形。
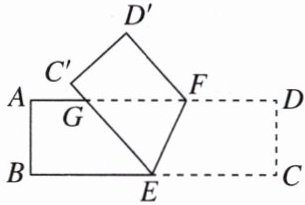
(1) 求$\angle CEF$的度数;
(2) 求证:$\triangle EFG$是等腰三角形。

答案:
(1)[解]
∵四边形ABCD是长方形,
∴AD//BC.
∴∠BEG=∠AGC'=48°.由折叠的性质,得∠CEF=∠C'EF,
∴∠CEF=$\frac{1}{2}$×(180°−48°)=66°.
(2)[证明]
∵AD//BC,
∴∠GFE=∠CEF.
∵∠CEF=∠C'EF,
∴∠GFE=∠C'EF.
∴△EFG是等腰三角形.
(1)[解]
∵四边形ABCD是长方形,
∴AD//BC.
∴∠BEG=∠AGC'=48°.由折叠的性质,得∠CEF=∠C'EF,
∴∠CEF=$\frac{1}{2}$×(180°−48°)=66°.
(2)[证明]
∵AD//BC,
∴∠GFE=∠CEF.
∵∠CEF=∠C'EF,
∴∠GFE=∠C'EF.
∴△EFG是等腰三角形.
8. 在下列三角形中,若$AB = AC$,则不能被一条直线分成两个小等腰三角形的是(
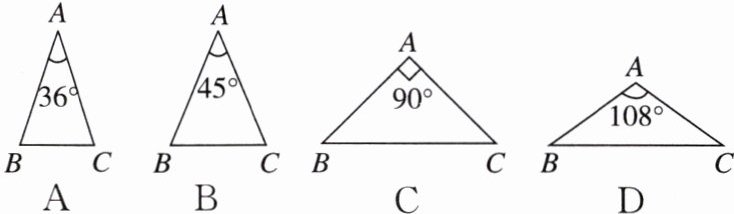
B
)
答案:
B
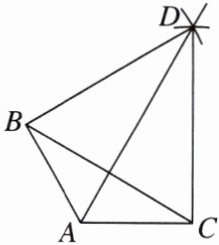
9. [2025邯郸期末]已知,在$\triangle ABC$中,$AB = AC$,如图,(1)分别以$B$,$C$为圆心,$BC$长为半径作弧,两弧交于点$D$;(2)作射线$AD$,连接$BD$,$CD$。根据以上过程及所作图形,下列结论中正确的个数为(
①$AD垂直平分BC$;
②$\angle BAD= \angle CAD$;
③$S_{四边形ABDC}= \frac{1}{2}AD\cdot BC$;
④$\triangle BCD$是等边三角形。
A.1
B.2
C.3
D.4
D
)①$AD垂直平分BC$;
②$\angle BAD= \angle CAD$;
③$S_{四边形ABDC}= \frac{1}{2}AD\cdot BC$;
④$\triangle BCD$是等边三角形。

A.1
B.2
C.3
D.4
答案:
D
查看更多完整答案,请扫码查看


