《2025年领先一步三维提优八年级数学上册苏科版》

6. (2024·南丹县期中)同学们玩过五子棋吗？它的比赛规则是只要同色5子先成一条直线就算胜。如图是两人玩的一盘棋,若白①的位置是$(1,-5)$,黑②的位置是$(2,-4)$,画出平面直角坐标系,现轮到黑棋走,你认为黑棋放在图中什么位置就获得胜利了？

答案：
画平面直角坐标系

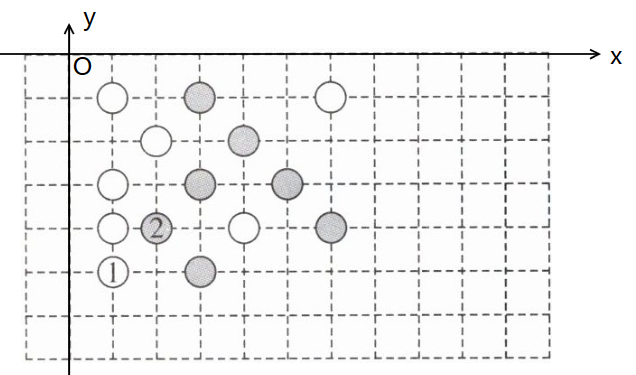
黑棋放在(2,0)或(7,-5)的位置就获得胜利了.

7. (2024·无锡经开区期末)如图,已知点A和点B的坐标分别为$(2,-3)和(-2,1)$
(1)在图中建立适当的平面直角坐标系；
(2)点C的坐标为______；
(3)网格中存在格点D,使得$\triangle CBD与\triangle BCA$全等,请写出所有符合条件的点D的坐标。

答案：

(1)；
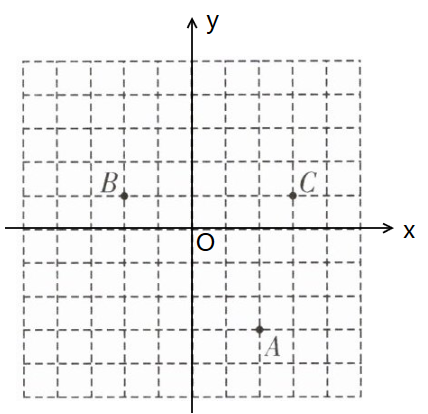(2)(3,1)；
(3)点D的坐标为(-1,-3)或(-1,5)或(2,5).

8. 在向红星镇居民介绍王家庄位置的时候,我们可以这样说,如图1,在以红星镇为原点,正东方向为x轴正方向,正北方向为y轴正方向的平面直角坐标系(1单位长度表示的实际距离为1km)中,王家庄的坐标为$(5,5)$；也可以说,王家庄在红星镇东北方向$5\sqrt{2}$km的地方。
还有一种方法广泛应用于航海、航空、气象、军事等领域。如图2,在红星镇所建的雷达站O的雷达显示屏上,把周角每$15^{\circ}$分成一份,正东方向为$0^{\circ}$,相邻两圆之间的距离为1个单位长度(1单位长度表示的实际距离为1km),现发现2个目标,我们约定用$(10,15^{\circ})$表示点M在雷达显示器上的坐标,则：
(1)点N可表示为______,王家庄位置可表示为______,点N关于雷达站点O成中心对称的点P的坐标为______；
(2)若有一家大型超市A在图中$(6,30^{\circ})$的地方,请直接标出点A,并将超市A与雷达站O连接,现准备在雷达站周围建立便民服务店B,使得$\triangle ABO为底角30^{\circ}$的等腰三角形,请直接写出点B在雷达显示屏上的坐标。(提示：$\sqrt{27}= 3\sqrt{3}$)

答案：

(1)(8,135°) (5√2,45°) (8,315°)；
(2)标出点A如图1所示: 点B在雷达显示屏上的坐标为(6,270°),(6,150°),(6√3,60°),(2√3,60°),(6√3,0°),(2√3,0°). 解析:如图2,分情况讨论如下: ①当OA=OB=6,且∠AOB=120°时,△ABO为底角30°的等腰三角形，此时有两种情况. a.当点B在点A逆时针120°时，点B₁的坐标为(6,150°); b.当点B在点A顺时针120°时，点B₂的坐标为(6,270°). ②当OA=AB=6,且∠OAB=120°时,△ABO为底角30°的等腰三角形，此时有两种情况. 过点A作AC⊥OB,垂足为点C,则OB=2OC. 在Rt△OAC中,∠AOC=30°,OA=6,
∴AC=$\frac{1}{2}$OA=3,
∴OC=$\sqrt{OA^{2}-AC^{2}}=\sqrt{27}=3\sqrt{3}$,
∴OB=2OC=6√3. c.当点B在点A逆时针30°时,点B₃的坐标为(6√3,60°); d.当点B在点A顺时针30°时，点B₄的坐标为(6√3,0°). ③当OB=AB,且∠ABO=120°时,△ABO为底角30°的等腰三角形，此时有两种情况. 过点B作BD⊥OA,垂足为点D,则OD=$\frac{1}{2}$OA=3. 在Rt△OBD中,∠BOD=30°,
∴OB=2BD. 设BD=x,则OB=2x,
∴OD=$\sqrt{OB^{2}-BD^{2}}=\sqrt{3}x$,
∴√3x=3,
∴x=√3,
∴OB=2√3. e.当点B在点A逆时针30°时,点B₅的坐标为(2√3,60°); f.当点B在点A顺时针30°时,点B₆的坐标为(2√3,0°). 综上可知,点B在雷达显示屏上的坐标为(6,270°),(6,150°),(6√3,60°),(2√3,60°),(6√3,0°),(2√3,0°).