第92页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. (2024·建湖县期中)综合与实践
【问题驱动】
如何验证勾股定理及探究勾股数?
【活动操作】
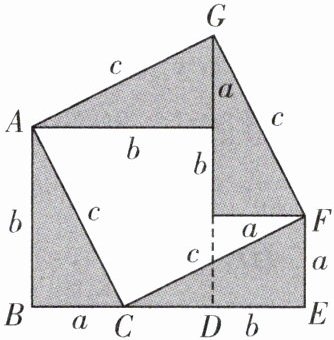
小明参照教材用 4 张全等的直角三角形纸片拼成如图所示的五边形 ABEFG.
【探索新知】
(1)从面积的角度思考,请用两种方法计算五边形 ABEFG 的面积,并写出得到等式 $ a^{2}+b^{2}= c^{2} $的过程.
(2)如果满足等式 $ a^{2}+b^{2}= c^{2} $的 $ a,b,c $是三个正整数,我们称 $ a,b,c $为勾股数. 已知 $ m,n $是正整数且 $ m>n $,证明:$ 2mn,m^{2}-n^{2},m^{2}+n^{2} $是勾股数.
【灵活运用】
(3)在如图所示的五边形 ABEFG 中,若 $ a= 4,b= 8 $,则空白部分的面积为
(4)请写出任意一组含有 85 的“勾股数”:
(5)小明在他找到的勾股数的表达式中,用 $ 2n^{2}+4n+4 $( $ n $为任意正整数)表示勾股数中的最大的一个数,则另两个数的表达式是
【问题驱动】
如何验证勾股定理及探究勾股数?
【活动操作】
小明参照教材用 4 张全等的直角三角形纸片拼成如图所示的五边形 ABEFG.
【探索新知】
(1)从面积的角度思考,请用两种方法计算五边形 ABEFG 的面积,并写出得到等式 $ a^{2}+b^{2}= c^{2} $的过程.
(2)如果满足等式 $ a^{2}+b^{2}= c^{2} $的 $ a,b,c $是三个正整数,我们称 $ a,b,c $为勾股数. 已知 $ m,n $是正整数且 $ m>n $,证明:$ 2mn,m^{2}-n^{2},m^{2}+n^{2} $是勾股数.
【灵活运用】
(3)在如图所示的五边形 ABEFG 中,若 $ a= 4,b= 8 $,则空白部分的面积为
48
.(4)请写出任意一组含有 85 的“勾股数”:
85,3612,3613
(答案不唯一).(5)小明在他找到的勾股数的表达式中,用 $ 2n^{2}+4n+4 $( $ n $为任意正整数)表示勾股数中的最大的一个数,则另两个数的表达式是
$2n^{2}+4n$
,$4n+4$
.
答案:
(1)如图所示:
方法一:$S_{五边形ABEFG}=S_{正方形ABDN}+S_{正方形NDEF}+S_{\triangle MFG}+S_{\triangle ANG}=b^{2}+a^{2}+\frac{1}{2}ab+\frac{1}{2}ab=a^{2}+b^{2}+ab$.
方法二:$S_{五边形ABEFG}=S_{正方形ACFG}+S_{\triangle ABC}+S_{\triangle CEF}=c^{2}+\frac{1}{2}ab+\frac{1}{2}ab=c^{2}+ab$,
$\therefore a^{2}+b^{2}+ab=c^{2}+ab$,$\therefore a^{2}+b^{2}=c^{2}$.
(2)$\because (2mn)^{2}=4m^{2}n^{2}$,$(m^{2}-n^{2})^{2}=m^{4}+n^{4}-2m^{2}n^{2}$,
$\therefore (2mn)^{2}+(m^{2}-n^{2})^{2}=m^{4}+n^{4}+2m^{2}n^{2}$.
$\because (m^{2}+n^{2})^{2}=m^{4}+n^{4}+2m^{2}n^{2}$,
$\therefore (2mn)^{2}+(m^{2}-n^{2})^{2}=(m^{2}+n^{2})^{2}$.
$\because m,n$是正整数且$m>n$,
$\therefore 2mn,m^{2}-n^{2},m^{2}+n^{2}$都是正整数,
$\therefore 2mn,m^{2}-n^{2},m^{2}+n^{2}$是勾股数.
(3)48 解析:$\because a=4,b=8$,$\therefore S_{五边形ABEFG}=a^{2}+b^{2}+ab=4^{2}+8^{2}+4×8=112$.又$\because S_{\triangle ABC}=\frac{1}{2}ab=\frac{1}{2}×4×8=16$,$\therefore S_{空白部分}=112 - 4×16=48$.
(4)85,3612,3613(答案不唯一)
(5)$2n^{2}+4n$ $4n+4$ 解析:$(2n^{2}+4n+4)^{2}=[(2n^{2}+4n)+4]^{2}=(2n^{2}+4n)^{2}+2×4×(2n^{2}+4n)+16=(2n^{2}+4n)^{2}+(16n^{2}+32n+16)=(2n^{2}+4n)^{2}+(4n+4)^{2}$,$\therefore$另两个表达式为$2n^{2}+4n$,$4n+4$.
(1)如图所示:
方法一:$S_{五边形ABEFG}=S_{正方形ABDN}+S_{正方形NDEF}+S_{\triangle MFG}+S_{\triangle ANG}=b^{2}+a^{2}+\frac{1}{2}ab+\frac{1}{2}ab=a^{2}+b^{2}+ab$.
方法二:$S_{五边形ABEFG}=S_{正方形ACFG}+S_{\triangle ABC}+S_{\triangle CEF}=c^{2}+\frac{1}{2}ab+\frac{1}{2}ab=c^{2}+ab$,
$\therefore a^{2}+b^{2}+ab=c^{2}+ab$,$\therefore a^{2}+b^{2}=c^{2}$.
(2)$\because (2mn)^{2}=4m^{2}n^{2}$,$(m^{2}-n^{2})^{2}=m^{4}+n^{4}-2m^{2}n^{2}$,
$\therefore (2mn)^{2}+(m^{2}-n^{2})^{2}=m^{4}+n^{4}+2m^{2}n^{2}$.
$\because (m^{2}+n^{2})^{2}=m^{4}+n^{4}+2m^{2}n^{2}$,
$\therefore (2mn)^{2}+(m^{2}-n^{2})^{2}=(m^{2}+n^{2})^{2}$.
$\because m,n$是正整数且$m>n$,
$\therefore 2mn,m^{2}-n^{2},m^{2}+n^{2}$都是正整数,
$\therefore 2mn,m^{2}-n^{2},m^{2}+n^{2}$是勾股数.
(3)48 解析:$\because a=4,b=8$,$\therefore S_{五边形ABEFG}=a^{2}+b^{2}+ab=4^{2}+8^{2}+4×8=112$.又$\because S_{\triangle ABC}=\frac{1}{2}ab=\frac{1}{2}×4×8=16$,$\therefore S_{空白部分}=112 - 4×16=48$.
(4)85,3612,3613(答案不唯一)
(5)$2n^{2}+4n$ $4n+4$ 解析:$(2n^{2}+4n+4)^{2}=[(2n^{2}+4n)+4]^{2}=(2n^{2}+4n)^{2}+2×4×(2n^{2}+4n)+16=(2n^{2}+4n)^{2}+(16n^{2}+32n+16)=(2n^{2}+4n)^{2}+(4n+4)^{2}$,$\therefore$另两个表达式为$2n^{2}+4n$,$4n+4$.
查看更多完整答案,请扫码查看


