《2025年领先一步三维提优八年级数学上册苏科版》

6. (2024·凉山州)匀速地向如图所示的容器内注水,直到把容器注满.在注水过程中,容器内水面高度$h随时间t$变化的大致图象是(C)

答案： C 解析:根据图象可知，容器的形状自下而上是小→大→中，则注水过程的水的高度是快→慢→中等，即每段的对应图象的倾斜度依次是倾斜度最大→倾斜度最小→倾斜度次之，四个选项中，C符合题意.

7. 已知等腰三角形的周长为10\ cm,将底边长y\ cm表示为腰长x\ cm的关系式是y = 10 - 2x,则其自变量x的取值范围是2.5＜ x＜5。

答案： $10 - 2x$ $2.5＜ x＜5$ 解析:$\because$等腰三角形的周长为10cm，底边长为$y cm$，腰长为$x cm$，$\therefore y + 2x = 10$，即$y = 10 - 2x$.$\because$底边长和腰长都是正数，$\therefore \begin{cases} x＞0 \\ 10 - 2x＞0 \end{cases}$，解得$0＜ x＜5$.由三角形的三边关系，得$x + x＞y$，即$x + x＞10 - 2x$，解得$x＞2.5$.$\therefore 2.5＜ x＜5$.

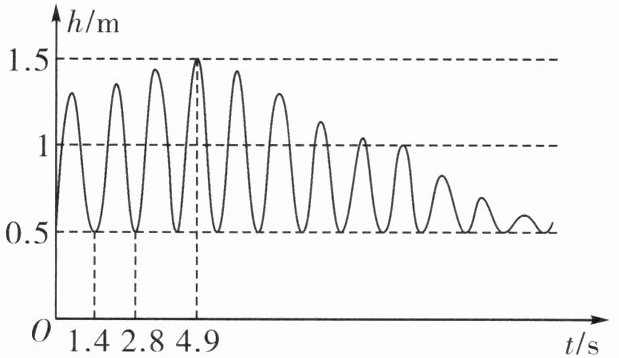
8. 小明帮助小芳荡秋千,在小明的助推下,秋千越来越高,秋千离地面的高度$h(m)与摆动时间t(s)$之间的关系如图所示.结合图象回答问题：
(1)根据函数定义,请判断变量$h是否为关于t$的函数？
(2)①秋千静止时离地面的距离是______$m$,秋千的最高点与地面距离是______$m$；
②______$s$后小明就不再助推小芳；
③从最低点开始向前和向后,再返回到最低点,这叫作一个周期,请问,小芳完成第一个周期用了______$s$；每个周期的时间是相等的,经过多长时间,秋千的最高点是$1\ m$？

答案：

(1)秋千离地面的高度$h$随摆动时间$t$的变化而变化，当$t$取一个确定的值时，$h$有唯一的值与它对应，$h$是$t$的函数，$t$是自变量.
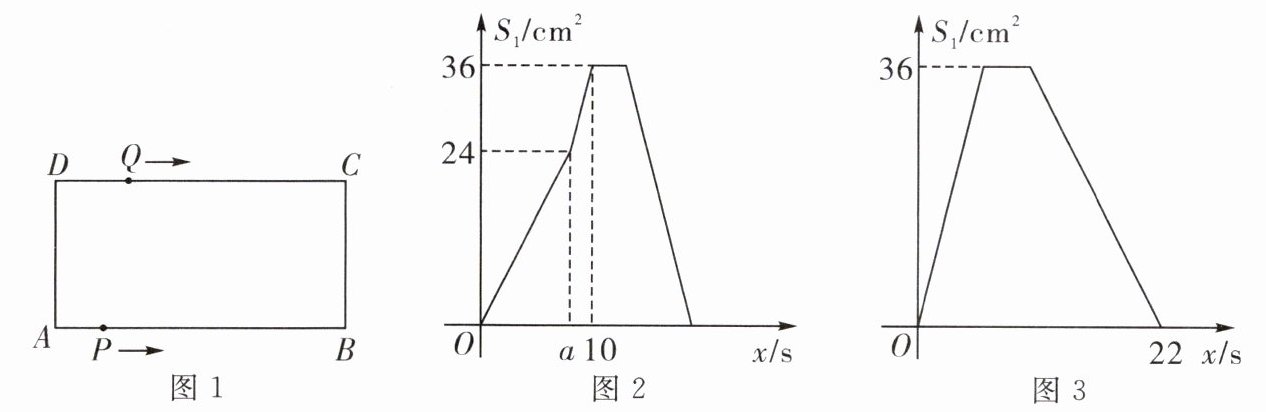
(2)①0.5 1.5 ②4.9 ③2.8 由题意，当经过4个周期后，第5个周期刚刚开始向前时，秋千的最高点是1m，如图所示 $\therefore 4×2.8 + 2.8÷4 = 11.9(s)$，$\therefore$经过11.9s，秋千的最高点是1m.

9. 如图1,在长方形$ABCD$中,$AB = 12\ cm$,$BC = 6\ cm$,点$P从点A$出发,沿$A\rightarrow B\rightarrow C\rightarrow D$路线运动,到点$D$停止；点$Q从点D$出发,沿$D\rightarrow C\rightarrow B\rightarrow A$运动,到点$A$停止.若点$P$,$Q$同时出发,点$P的速度为1\ cm/s$,点$Q的速度为2\ cm/s$,$a\ s时点P$,$Q$同时改变速度,点$P的速度变为b\ cm/s$,点$Q的速度变为c\ cm/s$.如图2是点$P出发x\ s后\triangle APD的面积S_1(cm^2)与x(s)$的函数关系图象；图3是点$Q出发x\ s后\triangle AQD的面积S_2(cm^2)与x(s)$的函数关系图象.
(1)求$a$,$b$,$c$的值；
(2)设点$P出发x(s)后离开点A的路程为y(cm)$,请写出$y与x$的函数关系式,并求出点$P与Q相遇时x$的值.

答案：
(1)由题意及题图2，得$S_{\triangle APD}=\dfrac{1}{2}PA\cdot AD=\dfrac{1}{2}(1\cdot a)\cdot6 = 24$，解得$a = 8$，$\therefore$点$P$变速前行驶的路程为$8×1 = 8(cm)$.由图2得，当$x = 10$时，$S_1 = 36 cm^2$.又$\because S_{\triangle ABD}=\dfrac{1}{2}AB\cdot AD = 36(cm^2)$，$\therefore$点$P$出发10s到点$B$，即点$P$出发10s时的路程为12cm，$\therefore 8×1+(10 - 8)b = 12$，解得$b = 2$.$\because$点$Q$变速前行驶的路程为$2×8 = 16(cm)$，$\therefore$点$Q$变速后行驶的路程为$12 + 6 + 12 - 16 = 14(cm)$.由题意及图3得，点$Q$变速后的行驶时间为$22 - 8 = 14(s)$，$\therefore 14c = 14$，解得$c = 1$.综上可知，$a$的值为8，$b$的值为2，$c$的值为1.
(2)当$0\leqslant x\leqslant8$时，$y = 1\cdot x$，即$y = x$；当$8＜ x\leqslant19$时，$y = 1×8 + 2(x - 8)$，即$y = 2x - 8$.则$y$与$x$的函数关系式为$y=\begin{cases} x(0\leqslant x\leqslant8) \\ 2x - 8(8＜ x\leqslant19) \end{cases}$.设点$Q$到点$A$需要走的路程为$y' cm$.当$8＜ x\leqslant19$时，$y' = 12 + 6 + 12 - 2×8 - 1×(x - 8)=22 - x(8＜ x\leqslant19)$.当$y = y'$时，点$P$与$Q$相遇，$\therefore 2x - 8 = 22 - x$，解得$x = 10$，$\therefore$点$P$与$Q$相遇时$x$的值为10.