《2025年领先一步三维提优八年级数学上册苏科版》

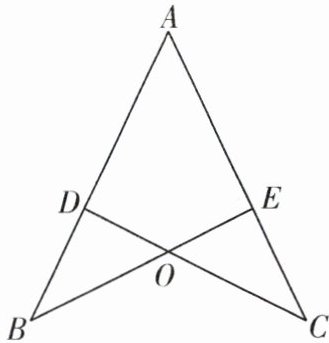
7. (2024·灌南县期中改编)如图,已知点 D 在 AB 上,点 E 在 AC 上,BE 和 CD 相交于点 O,AB = AC,BD = CE. 求证：△ABE≌△ACD.

答案：
∵BD=CE,AB=AC,
∴AB−BD=AC−CE,即AD=AE.
　在△ABE和△ACD中，{AB=AC,∠A=∠A,AE=AD,
∴△ABE≌△ACD(SAS).

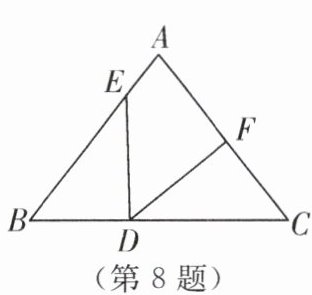
8. (2024·常州武进区期中)如图,△ABC 中,∠B = ∠C,BD = CF,BE = CD,∠EDF = α,则下列结论正确的是(A)

A.$2α + ∠A = 180^{\circ}$
B.$α + ∠A = 90^{\circ}$
C.$2α + ∠A = 90^{\circ}$
D.$α + ∠A = 180^{\circ}$

答案： A　解析:在△BDE和△CFD中,BE=CD,∠B=∠C,BD=CF,
∴△BDE≌△CFD(SAS),
∴∠BED=∠CDF.
∵∠A+∠B+∠C=180°,
∴2∠B=180°−∠A.
∵∠BDE+∠EDF+∠CDF=
　180°,
∴180°−∠B−∠BED+α+∠CDF=180°,
∴∠B=α,即180°−∠A=2α,整理,得2α+∠A=180°.

9. (2024·无锡梁溪区校级月考)如图,AB = AC,AD = AE,∠BAC = ∠DAE,∠1 = 25°,∠2 = 30°,则∠3 = 55°.

答案： 55

10. (2024·宿迁宿城区期中)如图,点 A,B,C,D 均在边长为 1 的正方形网格格点上,则∠1 + ∠2 的度数为____°.

答案：
45　解析:如图,在△ACB和△ECD中,BC=CD=1,∠ABC=∠EDC=90°,AB=DE=2,
∴△ACB≌△ECD(SAS),
∴∠1=∠CED,
∴∠1+∠2=∠BED=45°.
　　　　　　　　　　　　　　　　　　　　　

11. 如图,AD⊥AB,AE⊥AC,AD = AB,AE = AC,连接 BE 与 DC 交于点 M,则∠DMB = 90°.

答案： 90　解析:设AB,CD交于点N.
∵AD⊥AB,
　　AE⊥AC,
∴∠DAB=90°,∠EAC=90°,
∴∠DAB+∠BAC=∠EAC+∠BAC,即
　　∠DAC=∠BAE.又
∵DA=AB,AC=AE,
∴△DAC≌△BAE (SAS),
∴∠ADC=∠ABE.
∵∠AND=∠BNM,
∴∠DMB=
　　∠DAB=90°.

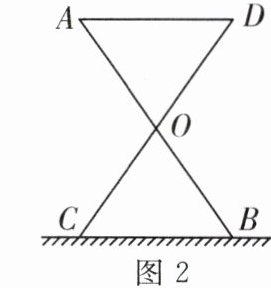
12. (2024·东海县期中)某中学计划为新生配备如图 1 所示的折叠凳,图 2 是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿 AB 和 CD 的长度相等,O 是它们的中点,为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度 AD 设计为 35 cm. 由以上信息你能求出 CB 的长吗？并说明理由.

答案： CB的长为35cm.理由如下:
∵O是AB,CD的中点，
∴OA=OB,OC=OD.
　　在△AOD和△BOC中,{OA=OB,∠AOD=∠BOC,OD=OC,
∴△AOD≌△BOC(SAS),
∴CB=AD.
　　又
∵AD=35cm,
∴CB=35cm.