《2025年领先一步三维提优八年级数学上册苏科版》

8. (2024·太仓市期中)已知在平面直角坐标系中,点$A$在第二象限,且到$x轴的距离为2$,到$y轴的距离为3$.
(1)点$A$的坐标为(-3,2)；
(2)点$B与点A关于y$轴对称,连接$AB$,点$C在直线AB上方且点C的坐标为(2,m)$,若$\triangle ABC的面积为12$,求$m$的值.
∵点B与点A关于y轴对称,
∴点B的坐标为(3,2).
∴AB=6.
∵点C在直线AB上方且点C的坐标为(2,m),
∴点C到直线AB的距离为m - 2.
又
∵△ABC的面积为12,
∴$\frac{1}{2}×6×(m - 2)=12$,解得m = 6.

答案：
(1)(-3,2)
(2)
∵点B与点A关于y轴对称,
∴点B的坐标为(3,2).
∴AB=6.
∵点C在直线AB上方且点C的坐标为(2,m),
∴点C到直线AB的距离为m - 2.
又
∵△ABC的面积为12,
∴$\frac{1}{2}×6×(m - 2)=12$,解得m = 6.

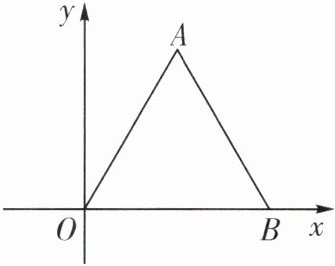
9. (2023·扬州邗江区期末)如图,$\triangle AOB是边长为2$的等边三角形,则点$A关于x$轴的对称点的坐标为(D)


A.$(-1,\sqrt{3})$
B.$(-1,-\sqrt{3})$
C.$(1,\sqrt{3})$
D.$(1,-\sqrt{3})$

答案： D 解析:过点A作AC⊥OB于点C.
∵△AOB是等边三角形,
∴OA = OB,OC = BC,$\angle OAC=\frac{1}{2}\angle OAB = 30^{\circ}$.又
∵OA = 2,
∴$OC=\frac{1}{2}OA = 1$,
∴$AC=\sqrt{AO^2 - OC^2}=\sqrt{2^2 - 1^2}=\sqrt{3}$,
∴点A的坐标是$(1,\sqrt{3})$,
∴点A关于x轴的对称点的坐标为$(1,-\sqrt{3})$.

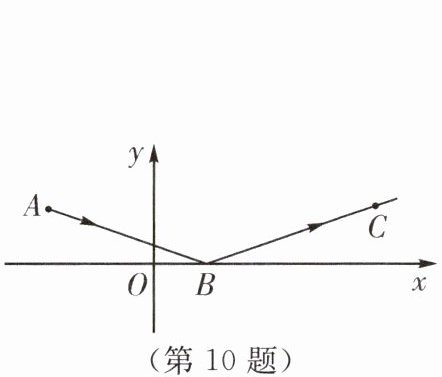
10. (2023·句容市期末)如图,一束光线从点A(-2,1)出发,经过x轴上的点B(1,0)反射后经过点C(m,n)(点A,点C是反射前后的对应点),则$\frac{1}{3}m - n= $$\frac{1}{3}$.
]

答案： $\frac{1}{3}$ 解析:由题意得,点A(-2,1)与点C(m,n)关于直线x = 1对称,
∴$1 - (-2)=m - 1$,n = 1,
∴m = 4,n = 1,
∴$\frac{1}{3}m - n=\frac{1}{3}×4 - 1=\frac{1}{3}$.

11. (2024·南通海门区校级月考)如图,在平面直角坐标系中,对$\triangle ABC$进行循环往复的轴对称变换,若原来点$A的坐标是(a,b)$,则经过第$2025次变换后所得点A$的坐标是______.((a,-b))

答案： (a,-b) 解析:
∵点A(a,b)前4次轴对称变换所得对应点的坐标依次为(a,-b),(-a,-b),(-a,b),(a,b),
∴每4次对称为一个循环组依次循环.
∵2025÷4 = 506……1,
∴经过第2025次变换后所得的点A与第1次变换的位置相同,在第四象限,坐标是(a,-b).

12. (2024·连云港海州区八校联考期末)如图,已知点$A和点B的坐标分别为(2,-4)和(-2,2)$.
(1)在图中建立适当的平面直角坐标系；
(2)点$C$的坐标为______,点$C关于x轴的对称点C'$的坐标为______；
(3)顺次连接$A$,$B$,$C$,得到$\triangle ABC$,点$D在y轴上且满足S_{\triangle ABC}= S_{\triangle DBC}$,请直接写出点$D$的坐标为______；
(4)已知点$E(-1,1)$,请在$x轴上找一点P$,使$PE + PC$的值最小,并求这个最小值.
]

答案：

(1)建立如图所示的平面直角坐标系:

(2)(3,2) (3,-2)
(3)(0,8)或(0,-4) 解析:设点D(0,m).
∵点A(2,-4),点B(-2,2),点C(3,2),
∴BC = 3 - (-2)=5,点A到BC的距离为2 - (-4)=6,点D到BC的距离为|m - 2|,
∴$S_{\triangle ABC}=\frac{1}{2}×5×6 = 15$,$S_{\triangle DBC}=\frac{1}{2}×|m - 2|×5=\frac{5}{2}|m - 2|$.又
∵$S_{\triangle ABC}=S_{\triangle DBC}$,
∴$15=\frac{5}{2}|m - 2|$,
∴|m - 2| = 6,
∴m = 8或m = -4,
∴点D的坐标为(0,8)或(0,-4).
(4)如图,找点E关于x轴的对称点E',连接CE',与x轴的交点即为所求的点P.
由对称,得PE = PE',
∴PE+PC = PE'+PC.
由“两点之间,线段最短”,得PE+PC≥CE'.
当点E',P,C三点共线时,PE+PC取最小值,即为CE'的长.
而$CE'=\sqrt{3^2 + 4^2}=5$,
∴PE+PC的最小值为5.