《2025年领先一步三维提优八年级数学上册苏科版》

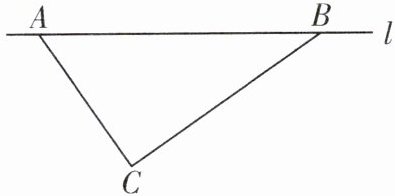
11. (2024·扬州江都区期中)如图,经过A村和B村(将A,B村看成直线l上的点)的笔直公路l旁有一块山地正在开发,现需要在C处进行爆破.已知C处与A村的距离为300m,C处与B村的距离为400m,且AC⊥BC.
(1)求A,B两村之间的距离;
(2)为了安全起见,爆破点C周围半径250m范围内不得进入,在进行爆破时,公路AB段是否有危险而需要封锁?如果需要,请计算需要封锁的路段长度;如果不需要,请说明理由.
]

答案：

(1)在Rt△ABC中,AC = 300 m,BC = 400 m,由勾股定理,得AB² = AC² + BC²,
∴AB² = 300² + 400² = 500²,
∴AB = 500.答:A,B两村之间的距离为500 m.
(2)公路AB有危险而需要封锁.求解如下:如图,过点C作CD⊥AB于点D.
　　　　　　　　　
∵S△ABC = $\frac{1}{2}$AB·CD = $\frac{1}{2}$BC·AC,
∴CD = $\frac{AC·BC}{AB}$ = $\frac{300×400}{500}$ = 240.
∵240 ＜ 250,
∴有危险,即AB段公路需要封锁.以点C为圆心,250 m为半径画弧,交AB于点E,F,连接CE,CF.由题意,得CE = CF = 250.在Rt△CDE中,由勾股定理,得CE² = DE² + CD²,
∴DE² = CE² - CD² = 250² - 240² = 70²,
∴DE = 70,
∴EF = 140.答:需要封锁的路段长度为140 m.

12. (2024·无锡锡山区期中)【项目主题】监控器如何布设才最优.
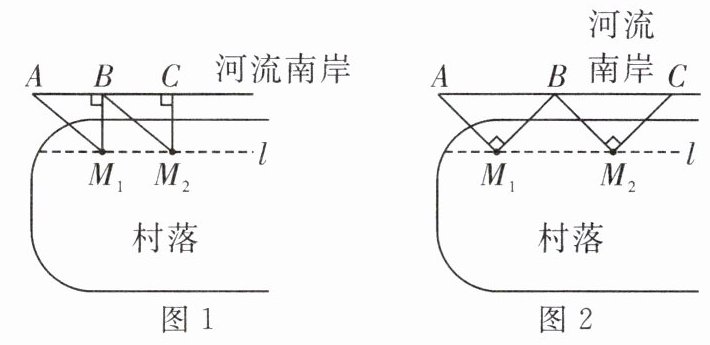
【项目背景】监控器的有效监测距离为500m,最大旋转角度为90°;村落、河流如图1所示,河流南岸长5000m;监控布设线l距离河流300m,l上任意两个监控$(M_1,M_2,…)$之间的距离相等.
【项目方案】
(1)方案1:如图1,从河流南岸边缘点A处起,使$AM_1= 500m,BM_1⊥AB,$即AB为监控器$M_1$监测范围;以此类推继续设置监控器,至少需要布设多少监控器?
(2)方案2:如图2,AB为监控器$M_1$监测范围,BC为监控器$M_2$监测范围$.AM_1⊥BM_1,BM_2⊥CM_2,$此时$BM_1= CM_2= 375m,$至少需要布设多少监控器?
(3)【项目总结】我认为方案_________是最优化方案.
]

答案：

(1)在Rt△ABM₁中,BM₁ = 300 m,AM₁ = 500 m,由勾股定理,得AB² + BM₁² = AM₁²,
∴AB = $\sqrt{AM₁² - BM₁²}$ = $\sqrt{500² - 300²}$ = 400(m).
∵村落与河流邻接长度为5000 m,且$\frac{5000}{400}$ = 12.5,
∴该水利部门至少需要布设13个监控器.
(2)如图,过点M₁作M₁N⊥AB于点N.
　　　　　　　　　　　　　　　　　　　　
由题意,得M₁N = 300 m.在Rt△M₁NB中,BM₁ = 375 m,由勾股定理,得BN² + M₁N² = BM₁²,
∴BN = $\sqrt{BM₁² - M₁N²}$ = $\sqrt{375² - 300²}$ = 225(m).设AN = x m,则AB = AN + BN = (225 + x)m.在Rt△AM₁N中,AM₁² = AN² + M₁N²,在Rt△ABM₁中,AM₁² + BM₁² = AB²,
∴AM₁² = AB² - BM₁².
∴AN² + M₁N² = AB² - BM₁²,
∴x² + 300² = (225 + x)² - 375²,解得x = 400,
∴AN = 400 m.在Rt△AM₁N中,由勾股定理,得AN² + M₁N² = AM₁²,
∴AM₁ = $\sqrt{AN² + M₁N²}$ = $\sqrt{400² + 300²}$ = 500(m).
∵监控器的有效监测距离为500 m,
∴符合题意,
∴AB = AN + NB = 400 + 225 = 625(m).
∵村落与河流邻接长度为5000 m,且$\frac{5000}{625}$ = 8,
∴该水利部门至少需要布设8个监控器.
(3)二