《2025年领先一步三维提优八年级数学上册苏科版》

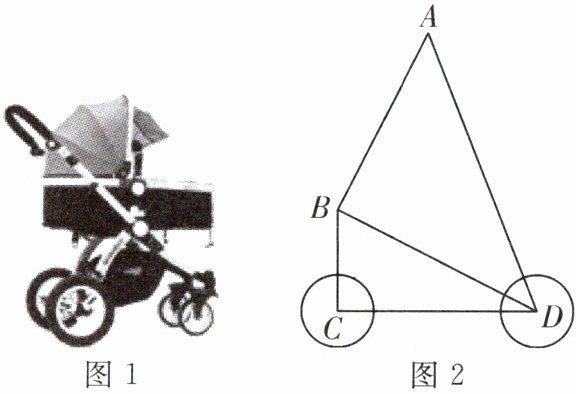
7. (2024·东台市期末)图1是某品牌婴儿车,图2为其简化结构示意图.现测得AB= CD= 8dm,BC= 4dm,AD= 12dm,其中AB与BD之间由一个固定角为90°的零件连接(即∠ABD= 90°).根据安全标准需满足BC⊥CD,请你通过计算说明该车是否符合安全标准

答案： 该婴儿车符合安全标准.计算过程如下:
∵∠ABD = 90°,AB = 8 dm,AD = 12 dm,
∴BD² = AD² - AB² = 12² - 8² = 80(dm²).
∵BC² = 4² = 16(dm²),CD² = 8² = 64(dm²),
∴BC² + CD² = 80,
∴BC² + CD² = BD²,
∴△BCD是直角三角形,
∴∠BCD = 90°,即BC⊥CD,
∴该婴儿车符合安全标准.

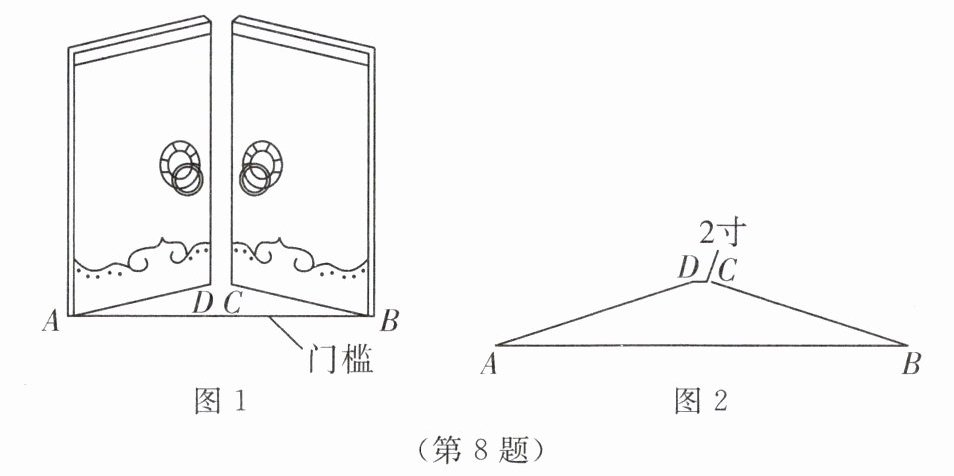
8. (2024·连云港海州区期中)《九章算术》是古代东方数学代表作,书中记载:今有开门去阃(读kǔn,门槛的意思)一尺,不合二寸,问门广几何?题目大意是:如图1,2(图2为图1的平面示意图),推开双门,双门间隙CD的距离为2寸,点C和点D距离门槛AB都为1尺(1尺= 10寸),则AB的长是( )

A.50.5寸
B.52寸
C.101寸
D.104寸

答案：
C 解析:如图,取AB的中点O,过点D作DE⊥AB于点E.由题意,得OA = OB = AD = BC = r寸,则AB = 2r寸,DE = 10寸,OE = $\frac{1}{2}$CD = $\frac{1}{2}$×2 = 1(寸),AE = (r - 1)寸.在Rt△ADE中,由勾股定理,得AE² + DE² = AD²,即(r - 1)² + 10² = r²,
∴2r = 101,
∴AB = 101寸.
　　　　　　　

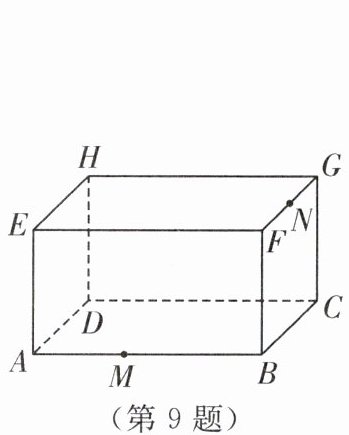
9. (2024·高青县期中)如图是放在地面上的一个长方体盒子,其中AB= 9,BC= 6,BF= 5,点M在棱AB上,且AM= 3,点N是FG的中点,一只蚂蚁沿着长方体盒子的表面从点M爬行到点N,它需要爬行的最短路程为______.

答案：
10 解析:由题意,分两种情形:①如图1,
∵AB = 9,AM = 3,BF = 5,
∴BM = 9 - 3 = 6,BN = 5 + 3 = 8,
∴MN = $\sqrt{BM² + BN²}$ = 10;②如图2,
∵AB = 9,AM = 3,BC = GF = 6,BF = 5,
∴PM = 9 - 3 + 3 = 9,PN = 5,
∴MN = $\sqrt{PM² + PN²}$ = $\sqrt{106}$.
∵10 ＜ $\sqrt{106}$,
∴它需要爬行的最短路程为10.
　　　　　 　　　　

10. (2024·盐城盐都区期中)金秋十月,某校体育运动会顺利举行,运动员们在赛场上奋力拼搏,老师们全力提供服务保障.如图,过道上A,B两点相距50m,C,D为两个班级,DA⊥AB于点A,CB⊥AB于点B,为方便同学们接取饮用水,现要在过道AB上临时设立一个饮水站E,使得C,D两个班级到E站的距离相等.
(1)请用直尺(不带刻度)和圆规画出饮水站E的位置;(不要求写作法,但要保留作图痕迹)
(2)已知AD= 30m,BC= 20m,求饮水站E到点B的距离.
]

答案：

(1)如图,点E即为所求.
　　　　　　　　　　
(2)由题意,得AB = 50 m.设BE = x m,则AE = (50 - x)m.
∵DA⊥AB,CB⊥AB,
∴∠A = ∠B = 90°.在Rt△BCE中,由勾股定理,得CE² = BC² + BE².在Rt△ADE中,由勾股定理,得DE² = AD² + AE².
∵DE = CE,
∴AD² + AE² = BC² + BE²,即30² + (50 - x)² = 20² + x²,解得x = 30,
∴BE = 30 m.答:饮水站E到点B的距离为30 m.