《2025年领先一步三维提优八年级数学上册苏科版》

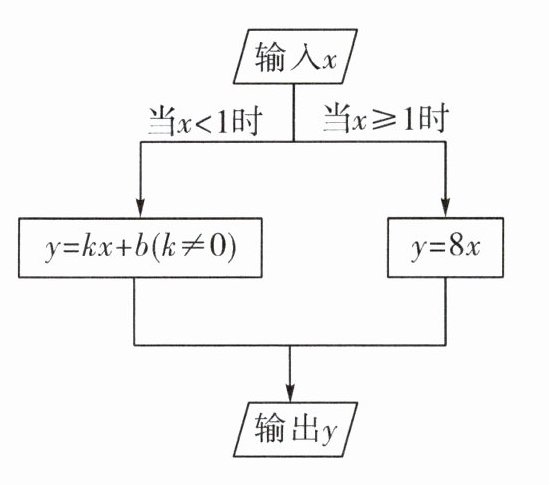
13. (2024 • 泗阳县一模)如图是一个“函数求值机”的示意图,其中 $ y $ 是 $ x $ 的函数. 下面表格中,是通过该“函数求值机”得到的几组 $ x $ 与 $ y $ 的对应值.

根据以上信息,解答下列问题：

(1)8当输入的 $ x $ 值为 $ 1 $ 时,输出的 $ y $ 值为______；
(2)求 $ k $,$ b $ 的值；
(3)当输出的 $ y $ 值为 $ 0 $ 时,求输入的 $ x $ 值.

答案：
(1)8
(2)由框图知,当x＜1时,框图执行y=kx+b(k≠0)的命令,
此时,当x=0时,y=6;当x=-2时,y=2……
则{2=-2k+b,
6=b,
解得{k=2,
b=6,
即k的值为2,b的值为6.
(3)令y=0,
当x≥1时,由y=8x,得0=8x,
∴x=0＜1(不符合题设,舍去);
当x＜1时,由y=2x+6,得0=2x+6,
∴x=-3＜1,
∴当输出的y值为0时,输入的x值为-3.

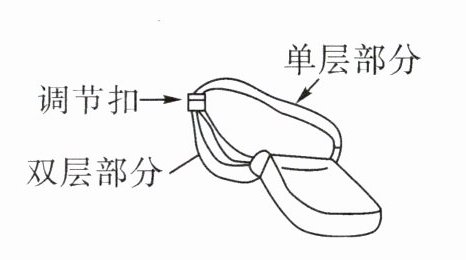
14. (2024 • 成都双流区期末改编)小明一家计划寒假外出旅游,为此,妈妈为小明准备了一个带有挎带的保温水杯,如图所示,水杯的挎带由双层部分、单层部分和调节扣构成,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短. 经测量单层部分的长度 $ x ( cm ) $ 与双层部分的长度 $ y ( cm ) $,得到如下表格中数据：


(1)已知 $ y $ 是 $ x $ 的一次函数,求出 $ y $ 关于 $ x $ 的函数表达式；
(2)当挎带的长度为 $ 110 \, cm $ 时,双层部分的长度为多少？
(3)若刚买回来的保温水杯的挎带全为双层,小明的身高最合适的挎带长度为 $ 126 \, cm $,请判断这个水杯是否适合小明？若适合,请说明调节挎带长度的方法；若不适合,请说明理由.

答案：
(1)设y关于x的函数表达式为y=kx+b.
由题意,得{40=60k+b,
34=72k+b,
解得{k=-0.5,
b=70,
∴y关于x的函数表达式是y=-0.5x+70.
(2)由题意,得x+y=110,
∴y=110-x.
由
(1),得y=-0.5x+70,
∴110-x=-0.5x+70,解得x=80,
∴y=110-x=110-80=30.
答:当挎带的长度为110 cm时,双层部分的长度为30 cm.
(3)由题意,得x+y=126,
∴y=126-x.
由
(1),得y=-0.5x+70,
∴126-x=-0.5x+70,解得x=112,
此时y=-0.5×112+70=14.
综上可知,这个水杯适合小明,调节挎带长度的方法为:将单层挎带的长度调整为112 cm,此时双层挎带的长度为14 cm.