《2025年领先一步三维提优八年级数学上册苏科版》

8. (2024 • 陕西)实验表明,在某地,温度在 $ 15 \, ^ { \circ } C $ 至 $ 25 \, ^ { \circ } C $ 的范围内,一种蟋蟀 $ 1 \, min $ 的平均鸣叫次数 $ y $ 可近似看成该地当时温度 $ x ( ^ { \circ } C ) $ 的一次函数. 已知这种蟋蟀在温度为 $ 16 \, ^ { \circ } C $ 时,$ 1 \, min $ 平均鸣叫 $ 92 $ 次；在温度为 $ 23 \, ^ { \circ } C $ 时,$ 1 \, min $ 平均鸣叫 $ 155 $ 次.
(1)求 $ y $ 关于 $ x $ 的函数表达式；
(2)当这种蟋蟀 $ 1 \, min $ 平均鸣叫 $ 128 $ 次时,该地当时的温度约是多少？

答案：
(1)由题意,设y=kx+b(k≠0).
当x=16,y=92,得92=16k+b;
当x=23,y=155,得155=23k+b.
解方程组{92=16k+b,
155=23k+b,
得{k=9,
b=-52,
∴y关于x的函数表达式为y=9x-52.
(2)当y=128时,128=9x-52,解得x=20.
答:该地当时的温度约是20℃.

9. 若 $ y $ 是 $ x $ 的正比例函数,$ x $ 是 $ z $ 的一次函数,则 $ y $ 是 $ z $ 的(C)
A.正比例函数
B.一次函数但不是正比例函数
C.正比例函数或一次函数
D.不构成函数关系

答案： C 解析:由题意,得y=kx,x=k₁z+b,则y=kk₁z+kb.当b≠0时,y是z的一次函数;当b=0时,y是z的正比例函数.

10. 某超市糯米的价格为 $ 5 $ 元/千克,立冬日推出促销活动：一次购买的数量不超过 $ 2 $ 千克时,按原价售出,超过 $ 2 $ 千克时,超过的部分打 $ 8 $ 折. 设某人的付款金额为 $ y $ 元,购买量为 $ x $ 千克,则付款金额 $ y $ 关于购买量 $ x ( x ＞ 10 ) $ 的函数表达式为y=4x+2.

答案： y=4x+2

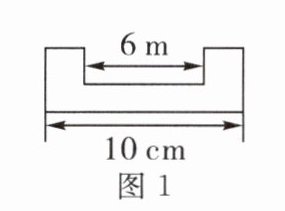
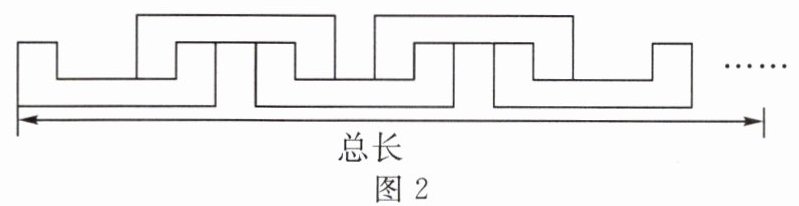
11. (2024 • 启东市期末)图 1 是一个轴对称图形,且每个角都是直角,长度如图 1 所示,小明用 $ x $ 个这样的图形,按照如图 2 所示的方法玩拼图游戏,两两相扣,相互间不留空隙. 则图形的总长度 $ y $ 关于图形个数 $ x $ 的函数表达式为______.


y=6x+4

答案： y=6x+4 解析:观察图形可知:当2个图拼接时,总长度为10+6=16;当3个图拼接时,总长度为10+2×6;…;以此类推,用x个这样的图形拼出来的图形总长度为10+6(x-1)=6x+4,
∴图形的总长度y关于图形个数x的函数表达式为y=6x+4.

12. (2024 • 盐城大丰区期末)经验表明,树在一定的成长阶段,其胸径(树主干的直径)越大,树就越高. 通过测量某种树,得到如表所示数据,已知树高 $ y $ 是其胸径 $ x $ 的一次函数.

(1)求树高 $ y ( m ) $ 关于其胸径 $ x ( m ) $ 的函数表达式；
(2)当这种树的胸径为 $ 0.46 \, m $ 时,其树高是多少？
(3)若这种树的胸径增长 $ 0.4 \, m $,则其树高增长多少？

答案：
(1)设y关于x的函数表达式为y=kx+b(k,b为常数,且k≠0).
当x=0.2,y=20,得20=0.2k+b;
当x=0.28,y=22,得22=0.28k+b.
解方程组{20=0.2k+b,
22=0.28k+b,
得{k=25,
b=15,
∴树高y(m)关于其胸径x(m)的函数表达式为y=25x+15.
(2)当x=0.46时,y=25×0.46+15=26.5.
答:当这种树的胸径为0.46 m时,其树高是26.5 m.
(3)设当胸径为x₁时,树高为y₁;当胸径为x₂时,树高为y₂.
由题意,得y₁=25x₁+15①,y₂=25x₂+15②,
②-①,得y₂-y₁=25(x₂-x₁).
当x₂-x₁=0.4时,y₂-y₁=25×0.4=10.
答:若这种树的胸径增长0.4 m,则其树高增长10 m.