第68页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
8. (2024·南通海门区期中)如图,面积为5的正方形ABCD的顶点A在数轴上,且点A表示的数为1,若$AD = AE$,则数轴上点E所表示的数为 (
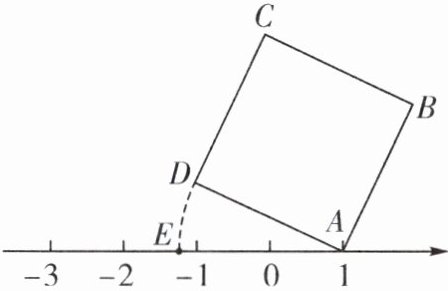
A.$-\sqrt{5}-1$
B.$-\sqrt{5}+1$
C.$\sqrt{5}+1$
D.$\sqrt{5}$
B
)
A.$-\sqrt{5}-1$
B.$-\sqrt{5}+1$
C.$\sqrt{5}+1$
D.$\sqrt{5}$
答案:
B解析:
∵正方形ABCD的面积为5,
∴边长为√5,即AD=√5.
∵AD=AE,
∴AE=√5.
∵点A表示的数为1,
∴数轴上点E所表示的数为-√5+1.
∵正方形ABCD的面积为5,
∴边长为√5,即AD=√5.
∵AD=AE,
∴AE=√5.
∵点A表示的数为1,
∴数轴上点E所表示的数为-√5+1.
9. (2024·启东市期中改编)在$\sqrt{1},\sqrt{2},\sqrt{3},…,\sqrt{2026}$这2026个数中,有理数的个数为m,无理数的个数为n,则$n - m$的平方根为
±44
.
答案:
±44 解析:
∵1²=1,2²=4,…,44²=1936,45²=2025,46²=2116 >2026,
∴原数据中共有45个数是有理数,即m=45,
∴无理数的个数为2026 - 45 = 1981,即n=1981,
∴n - m = 1936,
∴n - m的平方根为±44.
∵1²=1,2²=4,…,44²=1936,45²=2025,46²=2116 >2026,
∴原数据中共有45个数是有理数,即m=45,
∴无理数的个数为2026 - 45 = 1981,即n=1981,
∴n - m = 1936,
∴n - m的平方根为±44.
10. 已知实数a,b满足关系式$\vert a^{2}-9\vert+\sqrt{a^{2}-4b - 1}= 0$.判断$\sqrt[b]{a + 6}$是有理数还是无理数,并说明理由.
答案:
当a=3,b=2时,ⁿ√(a + 6)是有理数;当a=-3,b=2时,ⁿ√(a + 6)是无理数.理由如下:
∵|a² - 9|+√(a² - 4b - 1)=0,且|a² - 9|≥0,√(a² - 4b - 1)≥0,
∴a² - 9 = 0①,且a² - 4b - 1 = 0②,
由①,得a² = 9③,解得a = ±3.
将③代入②,得9 - 4b - 1 = 0,解得b = 2.
当a = 3,b = 2时,²√(3 + 6)=√9 = 3;
当a = -3,b = 2时,²√(-3 + 6)=√3.
综上可知,当a = 3,b = 2时,ⁿ√(a + 6)是有理数;当a = -3,b = 2时,ⁿ√(a + 6)是无理数.
∵|a² - 9|+√(a² - 4b - 1)=0,且|a² - 9|≥0,√(a² - 4b - 1)≥0,
∴a² - 9 = 0①,且a² - 4b - 1 = 0②,
由①,得a² = 9③,解得a = ±3.
将③代入②,得9 - 4b - 1 = 0,解得b = 2.
当a = 3,b = 2时,²√(3 + 6)=√9 = 3;
当a = -3,b = 2时,²√(-3 + 6)=√3.
综上可知,当a = 3,b = 2时,ⁿ√(a + 6)是有理数;当a = -3,b = 2时,ⁿ√(a + 6)是无理数.
11. (2024·北京海淀区校级期中)小兵喜欢研究数学问题,他设计了如下两种变换.
A变换:首先对实数取算术平方根,减去1;
B变换:首先对实数取立方根,然后取不超过该立方根的最大整数;
例如:实数7经过一次A变换得到$\sqrt{7}-1$,实数10经过一次B变换得到2.
(1) 实数25经过一次A变换所得的数是______,实数25经过一次B变换所得的数是______;
(2) 整数m经过两次B变换得到的数是2,则m的最小值是______,最大值是______;
(3) 实数x经过一次A变换得到的数是a,实数x经过一次B变换得到的数是b,是否存在x使得$a = b$成立? 若存在,请直接写出x的值;若不存在,请说明理由.
(1) 实数25经过一次A变换所得的数是
(2) 整数m经过两次B变换得到的数是2,则m的最小值是
(3) 实数x经过一次A变换得到的数是a,实数x经过一次B变换得到的数是b,是否存在x使得$a = b$成立? 若存在,请直接写出x的值;若不存在,请说明理由.
A变换:首先对实数取算术平方根,减去1;
B变换:首先对实数取立方根,然后取不超过该立方根的最大整数;
例如:实数7经过一次A变换得到$\sqrt{7}-1$,实数10经过一次B变换得到2.
(1) 实数25经过一次A变换所得的数是______,实数25经过一次B变换所得的数是______;
(2) 整数m经过两次B变换得到的数是2,则m的最小值是______,最大值是______;
(3) 实数x经过一次A变换得到的数是a,实数x经过一次B变换得到的数是b,是否存在x使得$a = b$成立? 若存在,请直接写出x的值;若不存在,请说明理由.
(1) 实数25经过一次A变换所得的数是
4
,实数25经过一次B变换所得的数是2
;(2) 整数m经过两次B变换得到的数是2,则m的最小值是
512
,最大值是19682
;(3) 实数x经过一次A变换得到的数是a,实数x经过一次B变换得到的数是b,是否存在x使得$a = b$成立? 若存在,请直接写出x的值;若不存在,请说明理由.
存在x=4或9使得a=b成立.
答案:
(1)4 2
(2)512 19682 解析:设m经过1次B变换得n,n再经过1次B变换得2.
∵不超过³√n的最大整数为2,
∴2 ≤ ³√n < 3,
∴8 ≤ n < 27.又
∵n为整数,
∴n的最小值为8,最大值为26.当n = 8时,不超过³√m的最大整数为8,
∴8 ≤ ³√m < 9,
∴8³ ≤ m < 9³,这时m的最小值为8³ = 512,最大值为9³ - 1 = 728;当n = 26时,不超过³√m的最大整数为26,
∴26 ≤ ³√m < 27,
∴26³ ≤ m < 27³,这时m的最小值为26³ = 17576,最大值为27³ - 1 = 19682.综上可知,m的最小值是512,最大值为19682.
(3)存在x = 4或9使得a = b成立.理由如下:
实数x经过1次A变换为a,则√x - 1 = a,
∴x = (a + 1)².
实数x经过1次B变换为b,则b ≤ √x < b + 1,
∴b³ ≤ x < (b + 1)³.
∴b³ ≤ (a + 1)² < (b + 1)³.
当a = b时,即a³ ≤ (a + 1)² < (a + 1)³,
由(a + 1)² < (a + 1)³,得(a + 1)² - (a + 1)³ < 0,
∴(a + 1)²[1 - (a + 1)] < 0,
即-a(a + 1)² < 0,
∴a(a + 1)² > 0.
又
∵(a + 1)² ≥ 0,
∴a > 0.
对于不等式a³ ≤ (a + 1)²,
当a = 1时,1³ < (1 + 1)²,不等式成立;
当a = 2时,2³ < (2 + 1)²,不等式成立;
当a = 3时,3³ < (3 + 1)²,不等式不成立,
之后a³越来越大,始终大于(a + 1)².
当a = 1时,x = (1 + 1)² = 4;
当a = 2时,x = (2 + 1)² = 9.
综上可知,存在x = 4或9使得a = b成立.
(1)4 2
(2)512 19682 解析:设m经过1次B变换得n,n再经过1次B变换得2.
∵不超过³√n的最大整数为2,
∴2 ≤ ³√n < 3,
∴8 ≤ n < 27.又
∵n为整数,
∴n的最小值为8,最大值为26.当n = 8时,不超过³√m的最大整数为8,
∴8 ≤ ³√m < 9,
∴8³ ≤ m < 9³,这时m的最小值为8³ = 512,最大值为9³ - 1 = 728;当n = 26时,不超过³√m的最大整数为26,
∴26 ≤ ³√m < 27,
∴26³ ≤ m < 27³,这时m的最小值为26³ = 17576,最大值为27³ - 1 = 19682.综上可知,m的最小值是512,最大值为19682.
(3)存在x = 4或9使得a = b成立.理由如下:
实数x经过1次A变换为a,则√x - 1 = a,
∴x = (a + 1)².
实数x经过1次B变换为b,则b ≤ √x < b + 1,
∴b³ ≤ x < (b + 1)³.
∴b³ ≤ (a + 1)² < (b + 1)³.
当a = b时,即a³ ≤ (a + 1)² < (a + 1)³,
由(a + 1)² < (a + 1)³,得(a + 1)² - (a + 1)³ < 0,
∴(a + 1)²[1 - (a + 1)] < 0,
即-a(a + 1)² < 0,
∴a(a + 1)² > 0.
又
∵(a + 1)² ≥ 0,
∴a > 0.
对于不等式a³ ≤ (a + 1)²,
当a = 1时,1³ < (1 + 1)²,不等式成立;
当a = 2时,2³ < (2 + 1)²,不等式成立;
当a = 3时,3³ < (3 + 1)²,不等式不成立,
之后a³越来越大,始终大于(a + 1)².
当a = 1时,x = (1 + 1)² = 4;
当a = 2时,x = (2 + 1)² = 9.
综上可知,存在x = 4或9使得a = b成立.
查看更多完整答案,请扫码查看


