《2025年领先一步三维提优八年级数学上册苏科版》

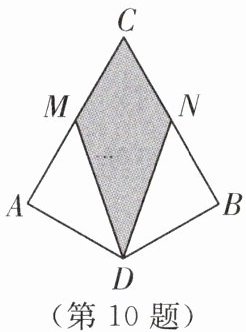
10. (2024·连云港海州区校级月考)如图,CA= CB,AD= BD,M,N分别是CA,CB的中点,若△ADM的面积为1.5,则图中阴影部分的面积为______.

3

答案： 3　解析:连接CD.在△ACD和△BCD中,
∵CA=CB,AD=BD,CD=CD,
∴△ACD≌△BCD(SSS),
∴S△ACD=S△BCD.
∵M,N分别是CA,CB的中点，
∴S△ADM=S△CDM=$\frac{1}{2}$S△ACD,S△BDN=S△CDN=$\frac{1}{2}$S△BCD,
∴S阴影=2S△ADM.
∵S△ADM=1.5,
∴S阴影=2×1.5=3.

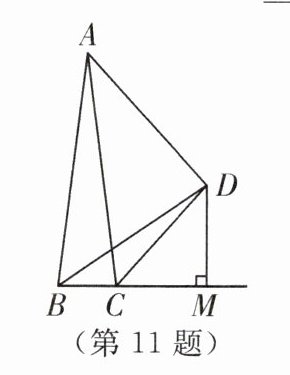
11. (2024·无锡锡山区期中)如图,B,C,E三点在同一条直线上,CD平分∠ACE,DB= DA,DM⊥BE于点M,若AC= 4,BC= $\frac{1}{2}$,则CM的长为______.

答案：
$\frac{7}{4}$　解析:如图,作DN⊥AC于点N.又
∵DM⊥BE,
∴∠DNC=∠DMC=90°.
∵CD平分∠ACE,
∴∠DCN=∠DCM.又
∵CD=CD,
∴△DCN≌△DCM(AAS),
∴CN=CM,DN=DM.又
∵AD=BD,
∴Rt△ADN≌Rt△BDM(HL),
∴AN=BM.
∵AN=AC−CN,BM=BC+CM,
∴AC−CN=BC+CM,
∴AC−CM=BC+CM,
∴2CM=AC−BC=4−$\frac{1}{2}$=$\frac{7}{2}$,
∴CM=$\frac{7}{4}$.

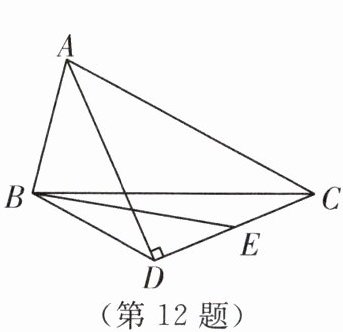
12. (2024·灌南县期中)如图,△ABC中,BC= 10,AC-AB= 6.过C作∠BAC的角平分线的垂线,垂足为D,点E为DC边的中点,连接BD,BE,则S△BEC的最大值为______.

答案：
7.5　解析:如图,延长AB,CD交于点F,
∵AD平分∠BAC,
∴∠CAD=∠FAD.
∵CD⊥AD,
∴∠ADC=∠ADF=90°.又
∵AD=AD,
∴△ADF≌△ADC(ASA),
∴AC=AF,DF=DC.
∵AC−AB=6,
∴AF−AB=6,即BF=6.
∵DF=DC,E是CD的中点，
∴S△BEC=$\frac{1}{4}$S△BFC.当BF⊥BC时,S△BFC最大,此时S△BEC也最大,最大值为$\frac{1}{4}$×$\frac{1}{2}$×10×6=7.5.

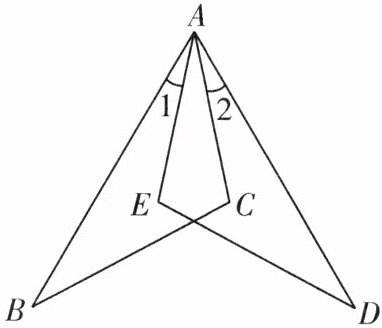
13. (2024·南京联合体期中)如图,AB= AD,∠C= ∠E,∠1= ∠2.求证：BC= DE.

答案：
∵∠1=∠2,
∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE.在△ABC和△ADE中,{∠C=∠E,∠BAC=∠DAE,AB=AD},
∴△ABC≌△ADE(AAS),
∴BC=DE.

14. (2024·滑县期末)小玉利用一根长3.6m的竿子来测量路灯AB的高度.她的方法如下：如图,在路灯前选一点P,使BP= 3.6m,并测得∠APB= 66°,然后把竖直的竿子CD(CD= 3.6m)在BP的延长线上左右移动,使∠CPD= 24°,此时测得BD= 11.6m.请根据这些数据,计算路灯AB的高度.

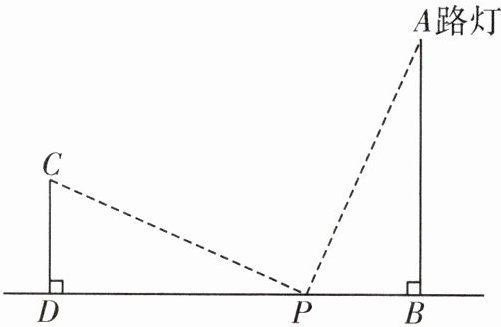
答案： 由题意,得∠CDP=∠PBA=90°.在Rt△PCD中,∠CPD=24°,
∴∠PCD=90°−24°=66°.
∵∠APB=66°,
∴∠PCD=∠APB.在△CPD和△PAB中,{∠CDP=∠PBA,CD=PB,∠PCD=∠APB},
∴△CPD≌△PAB(ASA),
∴PD=AB.
∵BD=11.6m,BP=3.6m,
∴AB=PD=BD−BP=8(m).答:路灯AB的高度是8m.

15. (2024·沭阳县期末)已知：a,b,c为△ABC的三边长,且a,b满足|2a-b+2|$+(a+b-8)^2= 0.$
(1)求c的取值范围；(2)在(1)的条件下,若2x-c= 1,求x的取值范围.

答案：
(1)
∵|2a−b+2|+(a+b−8)²=0,
∴{2a - b + 2 = 0,a + b - 8 = 0},解得{a = 2,b = 6}.又
∵a,b,c为△ABC的三边长,
∴6−2＜c＜6+2,即4＜c＜8,
∴c的取值范围为4＜c＜8.
(2)
∵2x−c=1,
∴c=2x−1,
∴4＜2x−1＜8,
∴2.5＜x＜4.5,即x的取值范围为2.5＜x＜4.5.