《2025年领先一步三维提优八年级数学上册苏科版》

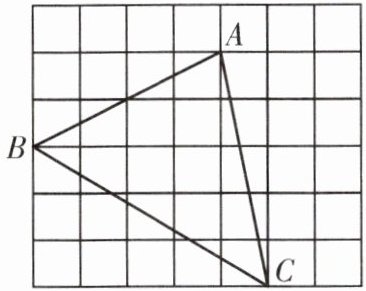
12. (2024·南京建邺区校级期中)如图,在边长为 $1$ 个单位长度的小正方形组成的网格中,$\triangle ABC$ 的三个顶点都在小正方形的顶点上.
(1)在图中利用无刻度直尺画出线段 $AB$ 的垂直平分线 $EF$；
(2)在图中利用无刻度直尺画出线段 $BC$ 的垂直平分线 $l$.
]

答案：

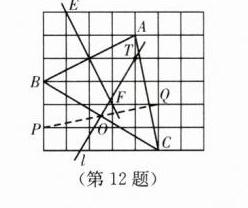
(1)如图，直线EF即为所求.
(2)如图，直线l即为所求.(取格点P，Q，连接PQ交BC于点O；取格点T，即TB=TC，作直线TO)

13. (2024·伊川县期末)【问题发现】我们知道“线段垂直平分线上点到线段两端的距离相等”,那么不在线段垂直平分线上的点到线段两端的距离大小如何判断呢？
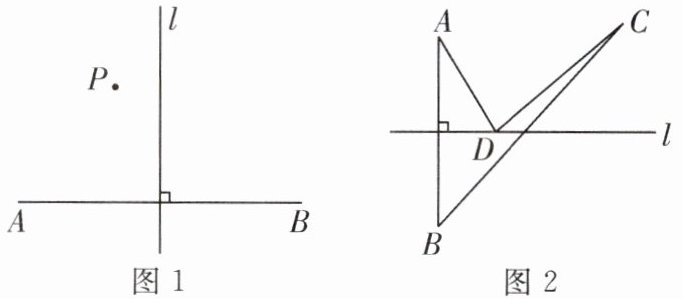
【自主研究】(1)如图 $1$,直线 $l$ 是线段 $AB$ 的垂直平分线,点 $P$ 在直线 $l$ 的左侧,经测量,$PA\lt PB$,请证明这个结论；
【迁移研究】(2)如图 $2$,直线 $l$ 是线段 $AB$ 的垂直平分线,点 $C$ 在直线 $l$ 外,且与点 $A$ 在直线 $l$ 的同侧,点 $D$ 是直线 $l$ 上的任意一点,连接 $AD$,$BC$,$CD$,试判断 $BC$ 和 $AD + CD$ 之间的大小关系,并说明理由.
]

答案：

(1)如图1，连接PB交直线l于点M，连接PA，AM.
∵直线l是线段AB的垂直平分线，
∴AM=BM，
∴PB=PM+MB=PM+AM.又
∵PM+AM＞PA，
∴PA＜PB.
(2)如图2，AD+CD≥BC.理由如下：①当点D不在线段BC上时，连接BD，
∵直线l是线段AB的垂直平分线，
∴AD=BD.
∵BD+CD＞BC，
∴AD+CD＞BC；②当点D在线段BC上时，AD+CD=BC.综上可知，AD+CD≥BC.

14. 在 $\triangle ABC$ 中,$BD$ 平分 $\angle ABC$.
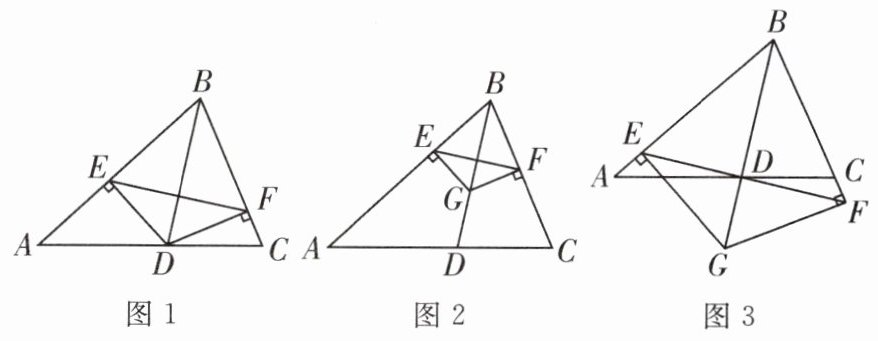
(1)如图 $1$,$DE\perp AB$ 于点 $E$,$DF\perp BC$ 于点 $F$,连接 $EF$,求证：$BD$ 垂直平分 $EF$；
(2)如图 $2$,当有一点 $G$ 从点 $D$ 向点 $B$ 运动时,$GE\perp AB$ 于点 $E$,$GF\perp BC$ 于点 $F$,此时(1)中的结论是否成立？请证明；
(3)如图 $3$,当点 $G$ 沿 $BD$ 方向从点 $D$ 沿 $BD$ 延长线运动时,$GE\perp AB$ 于点 $E$,$GF\perp BC$(或其延长线)于点 $F$,此时(1)中的结论是否成立？不需证明.
]

答案：
(1)
∵BD平分∠ABC，
∴∠EBD=∠FBD.
∵DE⊥AB于点E，DF⊥BC于点F，
∴∠BED=∠BFD=90°.在△EBD和△FBD中，$\left\{\begin{array}{l} ∠EBD=∠FBD,\\ ∠BED=∠BFD=90°,\\ BD=BD,\end{array}\right. $
∴△EBD≌△FBD(AAS)，
∴DE=DF，BE=BF，
∴BD垂直平分EF.
(2)
(1)中的结论仍然成立，即BD垂直平分EF.理由如下：
∵BD是∠ABC的平分线，
∴∠EBG=∠FBG.
∵GE⊥AB于点E，GF⊥BC于点F，
∴∠BEG=∠BFG=90°.在△EBG和△FBG中，$\left\{\begin{array}{l} ∠EBG=∠FBG,\\ ∠BEG=∠BFG=90°,\\ BG=BG,\end{array}\right. $
∴△EBG≌△FBG(AAS)，
∴GE=GF，BE=BF，
∴BD垂直平分EF.
(3)此时
(1)中的结论仍然成立.