《2025年领先一步三维提优八年级数学上册苏科版》

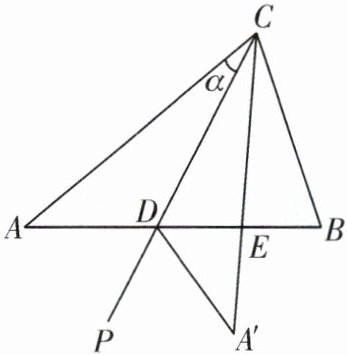
7. (2024·泗阳县期中)如图,$\triangle ABC$ 中,$\angle B = \angle ACB$,$\angle A = 40^{\circ}$,射线 $CP$ 从射线 $CA$ 开始绕点 $C$ 逆时针旋转 $\alpha$ 角 $(0^{\circ}＜\alpha＜70^{\circ})$,与射线 $AB$ 相交于点 $D$,将 $\triangle ACD$ 沿射线 $CP$ 翻折至 $\triangle A'CD$ 处,射线 $CA'$ 与射线 $AB$ 相交于点 $E$.
(1)若 $AB\perp CE$,求 $\angle\alpha$ 的度数；
(2)设 $\angle A'DB= \beta$,探究 $\alpha$,$\beta$ 之间的数量关系；
(3)若 $\triangle A'DE$ 是等腰三角形,请直接写出 $\angle\alpha$ 的度数.

答案：

(1)
∵AB⊥CE，
∴∠AEC = 90°。又
∵∠A = 40°，
∴∠ACE = 90° - 40° = 50°。由翻折，得∠ACE = 2∠α，
∴∠α = $\frac{1}{2}$∠ACE = $\frac{1}{2}$×50° = 25°。
(2)由题意，分两种情形:①当点A'在射线AB下方时，如图1所示。
∵∠A = 40°，∠ACD = α，
∴∠CDE = α + 40°。由折叠，得∠A' = ∠A = 40°，∠ADC = ∠A'DC。又
∵∠ADC = 180° - 40° - α = 140° - α，∠A'DC = α + 40° + β，
∴140° - α = α + 40° + β，即2α + β = 100°；②当点A'在射线AB上方时，如图2所示。
∵∠A = 40°，∠ACE = 2α，
∴∠CEA = 180° - 40° - 2α = 140° - 2α。又
∵∠CA'D = ∠A = 40°，
∴∠CEA + ∠A'DB = ∠CA'D，
∴140° - 2α + β = 40°，即2α - β = 100°。综上可知，α，β之间的数量关系为2α + β = 100°或2α - β = 100°。
　　　 　　
(3)①当点A'在射线AB下方时，如图1所示，此时∠DEA' = ∠ACA' + ∠A = 2α + 40°，且由
(2)①，知∠A'DB = 100° - 2α。若△A'DE是等腰三角形，则有下面3种情形:a.当∠DEA' = ∠A'时，则2α + 40° = 40°，解得α = 0°(舍去)；b.当∠DEA' = ∠EDA'时，则2α + 40° = 100° - 2α，解得α = 15°；c.当∠EDA' = ∠A'时，则100° - 2α = 40°，解得α = 30°。②当点A'在射线AB上方时，如图2所示。
∵∠CA'D = ∠A = 40°，
∴∠DA'E = 180° - 40° = 140°。若△A'DE是等腰三角形时，则只能∠A'DE = ∠A'ED = 20°。由
(2)②，知∠A'DE = 2α - 100°。
∴2α - 100° = 20°，解得α = 60°。综上可知，当△A'DE是等腰三角形，∠α的度数为15°或30°或60°。

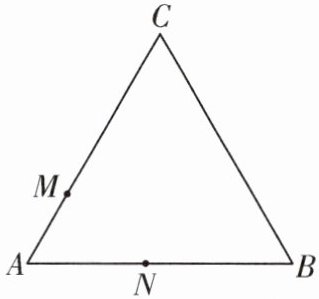
8. (2024·无锡锡山区期中)如图,$\triangle ABC$ 中,$AB = BC = CA = 12\mathrm{cm}$,现有两点 $M$,$N$ 分别从点 $A$,点 $B$ 同时出发,沿三角形的边顺时针运动,已知点 $M$ 的速度为 $2\mathrm{cm}/\mathrm{s}$,$N$ 的速度为 $4\mathrm{cm}/\mathrm{s}$. 当点 $N$ 第一次到达点 $B$ 时,$M$,$N$ 同时停止运动.
(1)点 $M$,$N$ 运动______秒后,$\triangle AMN$ 是等边三角形；
(2)点 $M$,$N$ 在边 $BC$ 上运动时,当 $\triangle AMN$ 是以 $MN$ 为底边的等腰三角形时,请求出此时 $M$,$N$ 运动的时间；
(3)点 $M$,$N$ 运动过程中,当 $\triangle AMN$ 是直角三角形时,请求出此时 $M$,$N$ 运动的时间.

答案：

(1)2　解析:设点M，N运动t s后，可得到△AMN是等边三角形，此时AM = t×2 = 2t(cm)，AN = AB - BN = (12 - 4t)cm。
∵△AMN是等边三角形，
∴2t = 12 - 4t，解得t = 2。
(2)设当点M，N在BC边上运动t s时，△AMN是以MN为底边的等腰三角形，如图1所示，由题意，得AN = AM，
∴∠AMN = ∠ANM，
∴180° - ∠AMN = 180° - ∠ANM，即∠AMC = ∠ANB。
∵AB = BC = AC，
∴△ACB是等边三角形，
∴∠C = ∠B。在△ACM和△ABN中，$\begin{cases} ∠AMC = ∠ANB \\ ∠C = ∠B \\ AC = AB \end{cases}$，
∴△ACM≌△ABN(AAS)，
∴CM = BN，
∴2t - 12 = 36 - 4t，解得t = 8，
∴CM = 2×8 - 12 = 4，BN = 36 - 4×8 = 4，符合题意。
∴点M，N在BC边上运动时，当△AMN是以MN为底边的等腰三角形时，此时M，N运动的时间为8 s。
　 　　 　　
(3)设运动的时间为t s。①当点N在AB上运动时，有两种情况:由题意，得BN = 4t cm，AM = 2t cm。
∵AB = 12 cm，
∴AN = (12 - 4t)cm。a.当△AMN是直角三角形，且∠AMN = 90°时，如图2所示。
∵∠A = 60°，
∴∠ANM = 90° - 60° = 30°，
∴AN = 2AM，即12 - 4t = 2×2t，解得t = 1.5；b.当△AMN是直角三角形，且∠ANM = 90°时，如图3所示。
∵∠A = 60°，
∴∠AMN = 90° - 60° = 30°，
∴AM = 2AN，即2t = 2(12 - 4t)，解得t = 2.4。②当点N在AC上运动时，点M也在AC上，此时A，M，N不能构成三角形。③当点N在BC上运动时，有两种情况:a.如图4，
∵△ABC是等边三角形，
∴当点N位于BC中点处时，AN⊥BC，即△AMN是直角三角形，则4t = 12 + 12 + 6，解得t = 7.5；b.如图5，
∵△ABC是等边三角形，
∴当点M位于BC中点处时，AM⊥BC，即△AMN是直角三角形，则2t = 12 + 6，解得t = 9。综上可知，当t = 1.5或2.4或7.5或9时，△AMN是直角三角形。