《2025年领先一步三维提优八年级数学上册苏科版》

4. (2024·泗洪县校级期中)如图,$\triangle ABC$中,$\angle C= 90^{\circ}$,$AB= 5\ cm$,$BC= 3\ cm$. 若动点$P从点C$开始,按$C\to A\to B\to C$的路径运动,且速度为每秒$1\ cm$,设出发的时间为$t\ s$. 问满足什么条件时($t$的值或取值范围),$\triangle BCP$为直角三角形？

答案：
由题意，分如下两种情况讨论：
① 当P在AC上运动（点P不与点C重合），即0 ＜ t ≤ 4时，
∠BCP = ∠BCA = 90°，
∴△BCP为直角三角形；
② 如图，当P在AB上，且CP⊥AB时，△BCP为直角三角形。
在Rt△ABC中，AB = 5cm，BC = 3cm，
由勾股定理，得BC² + AC² = AB²，
∴AC = √(AB² - BC²) = √(5² - 3²) = 4(cm)。
∵1/2AB·CP = 1/2AC·BC，
∴1/2×5CP = 1/2×3×4，
∴CP = 2.4cm。
在Rt△ACP中，由勾股定理，得AP² + CP² = AC²，
∴AP = √(AC² - CP²) = √(4² - 2.4²) = 3.2(cm)，
∴AC + AP = 4 + 3.2 = 7.2(cm)，
∴t = 7.2÷1 = 7.2。
综上可知，当0 ＜ t ≤ 4或t = 7.2时，△BCP为直角三角形。

5. (2024·泰州海陵区期中改编)如图,$C是线段AB$上一点,直线$AM\perp AB$,射线$CN\perp AB$,$AC= 3$,$BC= 2$,在直线$AM上取一点D$,在射线$CN上取一点E$,连接$BD$,$ED$,$BE$. 若$\triangle ABD与\triangle BDE$全等,求$CE$的值.

答案：
由题意，分两种情况讨论：
① 如图1，当点D在直线AB上方时，△ABD≌△EBD。
此时，BE = AB = AC + BC = 3 + 2 = 5。
在Rt△BCE中，BC = 2，由勾股定理，得BC² + CE² = BE²，
∴CE = √(BE² - BC²) = √(5² - 2²) = √21。

② 如图2，当点D在直线AB下方时，△ADB≌△EBD。
此时，DE = AB = 5，∠ABD = ∠EDB，
∴DK = BK，
∴DE - DK = AB - BK，即EK = AK。
设AK = EK = a，则DK = BK = 5 - a，CK = 3 - a。
在Rt△BCE中，由勾股定理，得BC² + CE² = BE²，
在Rt△KCE中，由勾股定理，得CK² + CE² = EK²，
∴CE² = BE² - BC² = EK² - CK²，
∴AD² - BC² = EK² - CK²，
∴DK² - AK² - BC² = EK² - CK²，
∴(5 - a)² - a² - 4 = a² - (3 - a)²，解得a = 15/8，
∴EK = 15/8，CK = 3 - 15/8 = 9/8，
∴CE = √(EK² - CK²) = √((15/8)² - (9/8)²) = 3/2。
综上可知，CE的值为√21或3/2。

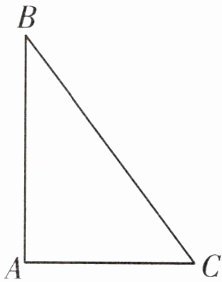
6. (2024·江阴市期中)如图,已知在$Rt\triangle ABC$中,$\angle A= 90^{\circ}$,$AC= 6$,$BC= 10$,有一动点$P从点A$出发,在折线段$AB-BC$上运动,速度为$2$个单位,运动时间$t$.
(1)当$t= $______时,$S_{\triangle ACP}= S_{\triangle BCP}$；
(2)若$CP平分\angle ACB$,求运动时间$t$；
(3)当$t$为何值时,$\triangle ACP$为轴对称图形？

答案：

(1) 2 解析：在Rt△ABC中，∠A = 90°，AC = 6，BC = 10，由勾股定理，得AB² + AC² = BC²，
∴AB = √(BC² - AC²) = √(10² - 6²) = 8。
当S△ACP = S△BCP时，1/2AC·AP = 1/2PB·AC，
∴6×2t = (8 - 2t)×6，解得t = 2，
∴当t = 2时，S△ACP = S△BCP。
(2) 如图1，过点P作PD⊥BC，垂足为D。
∵CP平分∠ACB，PD⊥BC，AP⊥AC，
∴AP = PD。
易证△APC≌△DPC(AAS)，则CD = AC = 6，
∴BD = BC - CD = 4。
在Rt△BPD中，由勾股定理，得BP² = PD² + BD²，
∴(8 - 2t)² = (2t)² + 4²，
∴t = 1.5。

(3) 由题意，分情况讨论如下：
① 当AP = AC时，△ACP为轴对称图形。
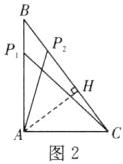
a. 如图2，当点P在边AB上时，AP₁ = AC = 6，
∴t = 6/2 = 3；
b. 如图2，当点P在边BC时，AP₂ = AC = 6。
过点A作AH⊥BC于点H，则CP₂ = 2CH。
∵S△ABC = 1/2AC·AB = 1/2BC·AH，
∴AH = (AC·AB)/BC = (6×8)/10 = 4.8。
在Rt△ACH中，由勾股定理，得AH² + CH² = AC²，
∴CH = √(AC² - AH²) = √(6² - 4.8²) = 3.6，
∴CP₂ = 2CH = 2×3.6 = 7.2，
∴t = (8 + 10 - 7.2)/2 = 5.4；
② 当AC = CP = 6时，t = (8 + 10 - 6)/2 = 6；
③ 当AP = CP时，如图3所示。
∵∠BAC = 90°，
∴∠B = 90° - ∠C，∠PAB = 90° - ∠PAC。
∵AP = CP，
∴∠PAC = ∠C，
∴∠PAB = ∠B，
∴BP = AP，
∴BP = AP = PC，
∴BP = 1/2BC = 5，
∴t = (8 + 5)/2 = 6.5。
综上可知，当t = 3或5.4或6或6.5时，△ACP为轴对称图形。