《2025年领先一步三维提优八年级数学上册苏科版》

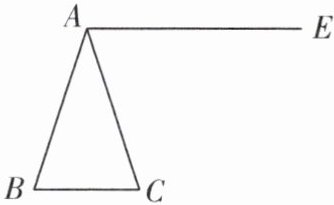
5. (2024·泰兴市期末)如图,$AB = AC$,$AE// BC$.
(1)用尺规作图:在射线 $AE$ 上找一点 $D$,连接 $BD$,使得 $\angle ADB= \frac{1}{2}\angle C$;(保留作图痕迹,说明作图理由)
(2)在(1)的条件下,若 $\angle C = 72^{\circ}$,$BD$ 与 $AC$ 相交于点 $F$,试判断 $\triangle ADF$ 的形状,并说明理由.

答案：
5.
(1)如图,以A为圆心,AB或AC为半径画弧交AE于点D,连接BD,点D即为所求.
理由:
∵AB=AC,AE//BC,
∴∠ABC=∠ACB,
∠ADB=∠CBD.
由作图,知AD=AB,
∴∠ADB=∠ABD,
∴∠CBD=∠ABD,
∴∠ABC=2∠ABD,
∴∠ACB=2∠ADB,
∴∠ADB=$\frac{1}{2}$∠ACB.
(2)△ADF是等腰三角形.理由如下:
∵∠ACB=72°,∠ADB=$\frac{1}{2}$∠ACB,
∴∠ADB=$\frac{1}{2}$×72°=36°.
又
∵AE//BC,
∴∠DAF=∠ACB=72°,
∴∠AFD=180° - ∠ADF - ∠DAF=72°,
∴∠DAF=∠DFA,
∴DA=DF,
∴△ADF是等腰三角形.

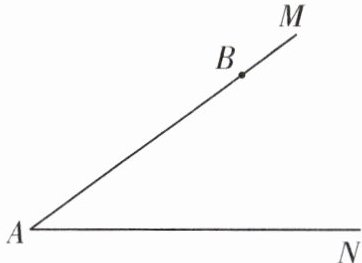
6. (2024·仪征市期中改编)尺规作图:如图,已知 $\angle MAN ＜ 45^{\circ}$,点 $B$ 是射线 $AM$ 上的一个定点,在射线 $AN$ 上求作点 $C$,使 $\angle ACB = 2\angle A$. (保留作图痕迹,并说明作图的理由)

答案：
6. 如图,作线段AB的垂直平分线l,直线l交射线AN于点D;以点B为圆心,BD长为半径作弧,交射线AN于另一点C,则点C即为所求.
理由:如图,连接BD,BC.
∵直线l为线段AB的垂直平分线,
∴DA=DB,
∴∠A=∠ABD,
∴∠BDC=∠A+∠ABD=2∠A.
∵BC=BD,
∴∠ACB=∠BDC,
∴∠ACB=2∠A.

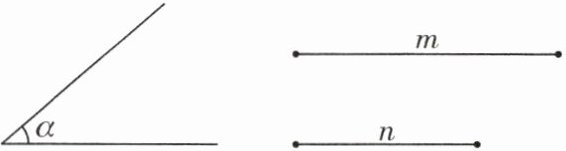
7. (2024·淮安市期末节选)如图,已知线段 $m$,$n$ 及 $\angle \alpha$.利用直尺和圆规求作所有满足条件的 $\triangle ABC$(全等除外),使得 $\angle B = \alpha$,$BC = m$,$AC = n$.(保留作图痕迹,不写作法)

答案：
7. 如图,作∠MBN=α,在射线BN上截取线段BC,使得BC=m;以C为圆心,n为半径作弧交BM于点A,A';连接AC,A'C,则△ABC,△A'BC即为所求.

8. (2024·南京秦淮区期末)已知线段 $a$,$b$,按下列要求用直尺和圆规作直角三角形.(要求:保留作图痕迹,写出必要的文字说明)

(1)作 $\triangle ABC$,使 $\angle A = 90^{\circ}$,$BC = a$,$AB = b$;
(2)作 $\triangle DEF$,使 $\angle D = 90^{\circ}$,$EF = a$,$DE - DF = b$.

答案：
8.
(1)如图1,作∠MAN=90°;在射线AN上截取线段AB,使得AB=b;以点B为圆心,a为半径作弧交AM于点C,则△ABC即为所求.
(2)如图2,作∠MON=45°;在ON的反向延长线上截取线段OE,使得OE=b;以点E为圆心,a为半径作弧交OM于点F;过点F作FD⊥ON于点D,则△DEF即为所求.