《2025年领先一步三维提优八年级数学上册苏科版》

4. (2024·丹阳市期中节选)如图, 等边三角形 $ABC$ 的边长为 $12$,$M$ 是边 $AC$ 上一动点 (与 $A$,$C$ 不重合),$N$ 是 $CB$ 延长线上一点, 且 $AM = BN$,$MN$ 交 $AB$ 于点 $D$. 将线段 $MN$ 绕点 $M$ 顺时针旋转 $60^{\circ}$ 得线段 $MF$, 连接 $FA$, 求 $FA^{2}$ 的最小值.

答案：
∵将线段MN绕点M顺时针旋转60°得线段MF,
∴FM=MN,∠FMN=60°,
∴∠AMF=180°-∠FMN-∠CMN=120°-∠CMN.
∵∠BNM=180°-∠C-∠CMN=120°-∠CMN,
∴∠AMF=∠BNM.
在△AMF和△BNM中,$\left\{\begin{array}{l} AM=BN,\\ ∠AMF=∠BNM,\\ FM=MN,\end{array}\right.$
∴△AMF≌△BNM(SAS),
∴FA=MB.
当MB⊥AC时,MB的值最小,此时FA的值最小,则FA²的值最小.
∵MB⊥AC,
∴∠BMC=90°.
在Rt△BMC中,BC=12,CM= $\frac{1}{2}$AC=6,
由勾股定理,得CM²+BM²=BC²,
∴BM²=BC²-CM²=12²-6²=108,
∴FA²的最小值为108.

5. (2024·南京金陵中学河西分校期中)数形结合就是把抽象的数学语言、数量关系与直观的几何图形、位置关系结合起来, 通过“以形助数”或“以数解形”可以使复杂问题简单化, 抽象问题具体化, 从而起到优化解题途径的目的.
【经历体验】(1)已知 $m$,$n$ 均为正实数, 且 $m + n = 4$, 求 $\sqrt{m^{2} + 1} + \sqrt{n^{2} + 4}$ 的最小值. 通过分析, 小明想到了利用下面的构造方法解决此问题: 如图的网格图中, 每个小正方形的边长为 $1$, 点 $A$,$B$,$C$,$D$ 在小正方形的顶点上, 点 $E$ 是线段 $AB$ 上的动点, 且不与端点重合, 连接 $CE$,$DE$, 设 $AE = m$, $BE = n$.
①用含 $m$ 的代数式表示 $CE = $____, 用含 $n$ 的代数式表示 $DE = $____;
②据此写出 $\sqrt{m^{2} + 1} + \sqrt{n^{2} + 4}$ 的最小值是____.
【类比应用】(2)根据上述的方法, 代数式 $\sqrt{x^{2} + 25} + \sqrt{(x - 16)^{2} + 49}$ 的最小值是____.
【感悟探索】(3)①已知 $a$,$b$,$c$ 为正数, 且 $a + b + c = 1$, 试运用构图法, 画出图形, 并写出 $\sqrt{a^{2} + b^{2}} + \sqrt{b^{2} + c^{2}} + \sqrt{a^{2} + c^{2}}$ 的最小值;
②若 $a$,$b$ 为正数, 则以 $\sqrt{a^{2} + b^{2}}$,$\sqrt{4a^{2} + 4b^{2}}$,$\sqrt{9a^{2} + b^{2}}$ 为边的三角形的面积是____.

答案：
【经历体验】
(1)①$\sqrt{m^{2}+1}$ $\sqrt{n^{2}+4}$
②5 解析:由①,得CE+DE= $\sqrt{m^{2}+1}+\sqrt{n^{2}+4}$.
∵CE+DE≥CD(当且仅当C,E,D共线时取等号),
∴CE+DE的最小值为CD的长.
如图1,连接CD,交AB于点E',即点E运动到点E'时,CE+DE取最小值.取格点F,构造Rt△CDF,由网格特征,得CF=3,DF=4,
∴CD= $\sqrt{3^{2}+4^{2}}=5$,即$\sqrt{m^{2}+1}+\sqrt{n^{2}+4}$的最小值为5.

【类比应用】
(2)20 解析:$\sqrt{x^{2}+25}+\sqrt{(x-16)^{2}+49}=\sqrt{x^{2}+5^{2}}+\sqrt{(x-16)^{2}+7^{2}}$.仿照
(1)中的方法,构造图形如图2所示,AC=5,AB=16,BD=7,设AE=x,则BE=16-x.在Rt△ACE中,由勾股定理,得CE= $\sqrt{AC^{2}+AE^{2}}=\sqrt{x^{2}+5^{2}}$,DE= $\sqrt{BE^{2}+BD^{2}}=\sqrt{(16-x)^{2}+7^{2}}$.
∵CE+DE≥CD(当且仅当C,E,D共线时取等号),
∴CE+DE的最小值为CD的长.连接CD,交AB于点E',即点E运动到点E'时,CE+DE取最小值.取格点F,构造Rt△CDF,由网格特征,得CF=12,DF=16,
∴CD= $\sqrt{12^{2}+16^{2}}=20$,即$\sqrt{x^{2}+25}+\sqrt{(x-16)^{2}+49}$的最小值为20.

【感悟探索】
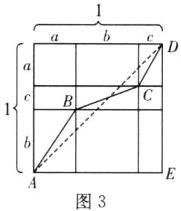
(3)①如图3,画出边长为1的正方形,在边上截取出长为a,b,c的线段,且使a+b+c=1.
由图及勾股定理,得AB= $\sqrt{a^{2}+b^{2}}$,BC= $\sqrt{b^{2}+c^{2}}$,CD= $\sqrt{a^{2}+c^{2}}$,
∴$\sqrt{a^{2}+b^{2}}+\sqrt{b^{2}+c^{2}}+\sqrt{a^{2}+c^{2}}=AB+BC+CD$.
∵AB+BC+CD≥AD(当且仅当A,B,C,D共线时取等号),
∴AB+BC+CD的最小值为AD的长.
连接AD,构造Rt△ADE,
在Rt△ADE中,DE=1,AE=1,
由勾股定理,得AE²+DE²=AD²,
∴AD= $\sqrt{1^{2}+1^{2}}=\sqrt{2}$,即AB+BC+CD的最小值为$\sqrt{2}$,
∴$\sqrt{a^{2}+b^{2}}+\sqrt{b^{2}+c^{2}}+\sqrt{a^{2}+c^{2}}$的最小值为$\sqrt{2}$.

②2ab 解析:如图4,构造长为3a,宽为2b的长方形ABCD,点E在AD上,且AE=a,点F在AB上,且AF=b.由图及勾股定理,得EF= $\sqrt{a^{2}+b^{2}}$,CE= $\sqrt{(2a)^{2}+(2b)^{2}}=\sqrt{4a^{2}+4b^{2}}$,CF= $\sqrt{(3a)^{2}+b^{2}}=\sqrt{9a^{2}+b^{2}}$,
∴以$\sqrt{a^{2}+b^{2}}$,$\sqrt{4a^{2}+4b^{2}}$,$\sqrt{9a^{2}+b^{2}}$为边的三角形的面积等于△CEF的面积.
∵S△CEF=S长方形ABCD-S△AEF-S△CDE-S△BCF=3a×2b- $\frac{1}{2}$×a×b- $\frac{1}{2}$×2a×2b- $\frac{1}{2}$×3a×b=2ab.