第79页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
5. (2024·南通)“赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的两条直角边长分别为$ m,n(m>n) $.若小正方形面积为$ 5,(m+n)^{2}= 21 $,则大正方形面积为(
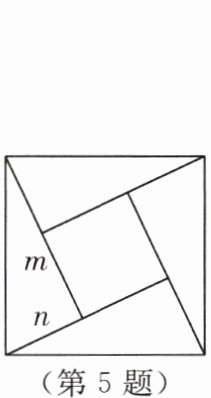
A.12
B.13
C.14
D.15
B
)
A.12
B.13
C.14
D.15
答案:
B
6. 数学家欧几里得利用如图的图形验证了勾股定理.以 Rt△ABC 的三条边为边长向外作正方形 ABED ,正方形 ACHI ,正方形 BCGF ,连接 CE .若 BC= 8,AB= 10 ,则 △BCE 的面积为
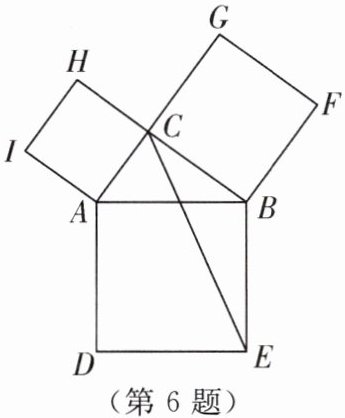
32
.
答案:
32 解析:连接 AF.
∵在$Rt△ABC$中,$BC=8,AB=10,\therefore AC=\sqrt {AB^{2}-BC^{2}}=6,\therefore S_{△ABC}=\frac {1}{2}×6×8=24$.由题意,得$AB=EB,BF=BC,∠ABE=∠CBF=90^{\circ },\therefore ∠ABE+∠ABC=∠CBF+∠ABC$,即$∠EBC=∠ABF,\therefore △BCE\cong △BFA(SAS).$
又$\because BF=BC=8,\therefore S_{△BCE}=S_{△BFA}=64+24-\frac {1}{2}×(8+6)×8=32.$
∵在$Rt△ABC$中,$BC=8,AB=10,\therefore AC=\sqrt {AB^{2}-BC^{2}}=6,\therefore S_{△ABC}=\frac {1}{2}×6×8=24$.由题意,得$AB=EB,BF=BC,∠ABE=∠CBF=90^{\circ },\therefore ∠ABE+∠ABC=∠CBF+∠ABC$,即$∠EBC=∠ABF,\therefore △BCE\cong △BFA(SAS).$
又$\because BF=BC=8,\therefore S_{△BCE}=S_{△BFA}=64+24-\frac {1}{2}×(8+6)×8=32.$
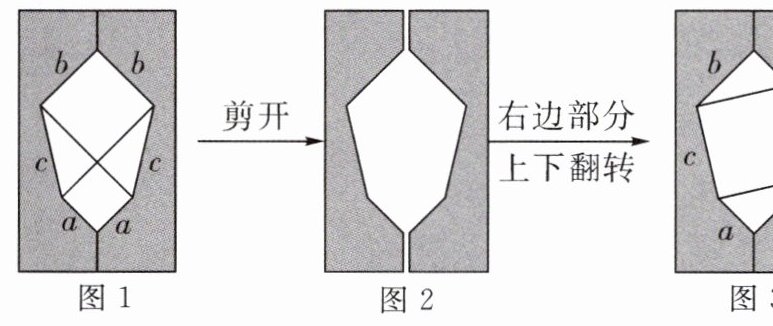
7. (2024·中牟县期末改编)古往今来,人们对勾股定理的证明一直保持着极大的热情.意大利著名画家达·芬奇用如图所示的方法证明了勾股定理,其中图1的空白部分是由两个正方形和两个直角三角形组成,图3的空白部分由两个直角三角形和一个正方形组成.设图1中空白部分的面积为$ S_{1} $,图3中空白部分的面积为$ S_{2} $.请利用达·芬奇的方法证明勾股定理.

答案:
由题意及图形,得$S_{1}=a^{2}+b^{2}+2×\frac {1}{2}ab=a^{2}+b^{2}+ab,$
$S_{2}=c^{2}+2×\frac {1}{2}ab=c^{2}+ab.$
$\because S_{1}=S_{2},\therefore a^{2}+b^{2}+ab=c^{2}+ab,\therefore a^{2}+b^{2}=c^{2}.$
$S_{2}=c^{2}+2×\frac {1}{2}ab=c^{2}+ab.$
$\because S_{1}=S_{2},\therefore a^{2}+b^{2}+ab=c^{2}+ab,\therefore a^{2}+b^{2}=c^{2}.$
8. (2024·连云港赣榆区期中)如图,$ AB⊥BC,DC⊥BC $,垂足分别为$ B,C $,点$ E 为线段 BC $上一点,且$ AB= EC,AC= DE,DE 交 AC 于点 F $.
(1)求证:$ AC⊥DE $;
(2)连接$ AD $,若$ AB= a,BC= b,AC= c $,通过用不同方法计算四边形$ ABCD $的面积,验证勾股定理.
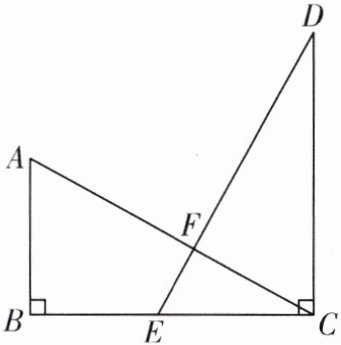
(1)求证:$ AC⊥DE $;
(2)连接$ AD $,若$ AB= a,BC= b,AC= c $,通过用不同方法计算四边形$ ABCD $的面积,验证勾股定理.

答案:
(1)$\because AB⊥BC,DC⊥BC,\therefore ∠ABC=∠ECD=90^{\circ }.$
在$Rt△ABC$和$Rt△ECD$中,$\left\{\begin{array}{l} AC=ED,\\ AB=EC,\end{array}\right. $
$\therefore △ABC\cong △ECD(HL),\therefore ∠CAB=∠DEC.$
$\because ∠ABC=90^{\circ },\therefore ∠CAB+∠BCA=90^{\circ },\therefore ∠DEC+∠BCA=90^{\circ },$
$\therefore ∠EFC=90^{\circ }$,即$AC⊥DE.$
(2)如图,连接 AE,AD.

由
(1),知$△ABC\cong △ECD,$
$\therefore EC=AB=a,DC=BC=b,DE=AC=c,BE=b-a,$
$\therefore S_{四边形ABCD}=\frac {1}{2}(a+b)b=\frac {1}{2}ab+\frac {1}{2}b^{2}.$
$\because AC⊥DE,$
$\therefore S_{四边形AECD}=S_{△ADC}+S_{△AEC}=\frac {1}{2}AC\cdot DF+\frac {1}{2}AC\cdot EF=\frac {1}{2}AC\cdot (DF+EF)=\frac {1}{2}AC\cdot DE=\frac {1}{2}c^{2},$
$\therefore S_{四边形ABCD}=S_{四边形AECD}+S_{△ABE}=\frac {1}{2}c^{2}+\frac {1}{2}a(b-a)=\frac {1}{2}c^{2}+\frac {1}{2}ab-\frac {1}{2}a^{2},$
$\therefore \frac {1}{2}ab+\frac {1}{2}b^{2}=\frac {1}{2}c^{2}+\frac {1}{2}ab-\frac {1}{2}a^{2}$,化简,得$a^{2}+b^{2}=c^{2}.$
(1)$\because AB⊥BC,DC⊥BC,\therefore ∠ABC=∠ECD=90^{\circ }.$
在$Rt△ABC$和$Rt△ECD$中,$\left\{\begin{array}{l} AC=ED,\\ AB=EC,\end{array}\right. $
$\therefore △ABC\cong △ECD(HL),\therefore ∠CAB=∠DEC.$
$\because ∠ABC=90^{\circ },\therefore ∠CAB+∠BCA=90^{\circ },\therefore ∠DEC+∠BCA=90^{\circ },$
$\therefore ∠EFC=90^{\circ }$,即$AC⊥DE.$
(2)如图,连接 AE,AD.

由
(1),知$△ABC\cong △ECD,$
$\therefore EC=AB=a,DC=BC=b,DE=AC=c,BE=b-a,$
$\therefore S_{四边形ABCD}=\frac {1}{2}(a+b)b=\frac {1}{2}ab+\frac {1}{2}b^{2}.$
$\because AC⊥DE,$
$\therefore S_{四边形AECD}=S_{△ADC}+S_{△AEC}=\frac {1}{2}AC\cdot DF+\frac {1}{2}AC\cdot EF=\frac {1}{2}AC\cdot (DF+EF)=\frac {1}{2}AC\cdot DE=\frac {1}{2}c^{2},$
$\therefore S_{四边形ABCD}=S_{四边形AECD}+S_{△ABE}=\frac {1}{2}c^{2}+\frac {1}{2}a(b-a)=\frac {1}{2}c^{2}+\frac {1}{2}ab-\frac {1}{2}a^{2},$
$\therefore \frac {1}{2}ab+\frac {1}{2}b^{2}=\frac {1}{2}c^{2}+\frac {1}{2}ab-\frac {1}{2}a^{2}$,化简,得$a^{2}+b^{2}=c^{2}.$
查看更多完整答案,请扫码查看


