《2025年领先一步三维提优八年级数学上册苏科版》

1. (2024·临夏州)下列各数中,是无理数的是(A)
A.$\dfrac{\pi}{2}$
B.$\dfrac{1}{3}$
C.$\sqrt[3]{27}$
D.$0.13133$

答案： A

2. (2024·扬州邗江区一模)估计21的算术平方根介于(D)
A.1和2之间
B.2和3之间
C.3和4之间
D.4和5之间

答案： D

3. (2024·东台市期中)请你写出一个无理数$a$,使得$0 ＜ a ＜ 1$,则$a$为$\frac{\pi}{4}$(答案不唯一).

答案： $\frac{\pi}{4}$(答案不唯一)

4. (2024·南京鼓楼区一模)与无理数$\sqrt{15}$最接近的正整数是4.

答案： 4

5. (1)(2024·资阳改编)若$\sqrt{5} ＜ m ＜ \sqrt{10}$,则整数$m$的值为3；
(2)(2024·苏州工业园区期中)比$\sqrt{3}大且比\sqrt{14}$小的所有整数的和是5.

答案：
(1)3
(2)5

6. 将下列各数按要求填入相应的圆圈里：
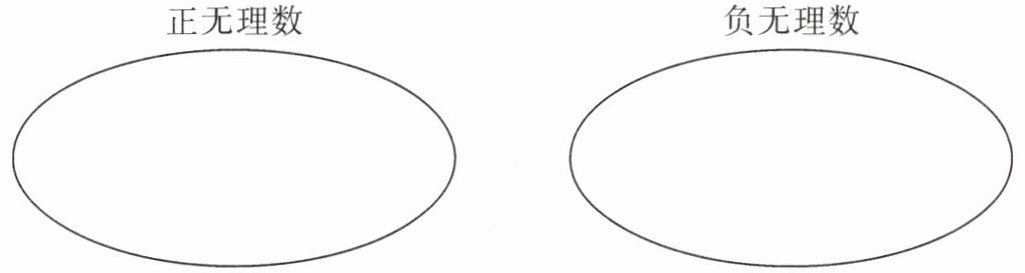
$\dfrac{22}{7},-\pi,\sqrt[3]{64},1.41414,\sqrt{8},|-7+\pi|,\sqrt[3]{-36},-\sqrt{1.6},\dfrac{\sqrt{3}}{2},\sqrt{(-0.6)^2}$.

答案： $\sqrt[3]{64}=4$，$|-7+\pi|=7-\pi$，$\sqrt{(-0.6)^2}=0.6$.
按要求填数如下所示：
正无理数：$\sqrt{8}$，$|-7+\pi|$，$\frac{\sqrt{3}}{2}$ 负无理数：$-\pi$，$\sqrt[3]{-36}$，$-\sqrt{1.6}$

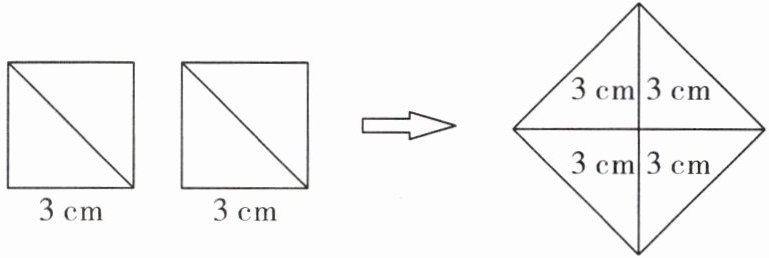
7. 若小明想将两块边长都为$3\mathrm{cm}$的正方形纸板沿对角线剪开,拼成如图所示的一个大正方形,请你帮他求出这个大正方形的面积.它的边长是整数吗？若不是整数,则请你估计这个边长的值在哪两个整数之间.

答案： 由题意，得$S_{大正方形}=3^2+3^2=18(cm^2)$，
则大正方形的边长为$\sqrt{18}\ cm$.
$\because \sqrt{18}$不能写成某个有理数的平方，$\therefore \sqrt{18}$不是整数.
$\because \sqrt{16}＜\sqrt{18}＜\sqrt{25}$，$\therefore 4＜\sqrt{18}＜5$，
$\therefore$大正方形边长的值在整数4和5之间.