《2025年领先一步三维提优八年级数学上册苏科版》

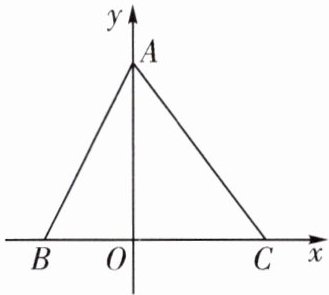
6. (2024·昆山市校级月考)如图,在平面直角坐标系中,点 $A$ 的坐标为 $(0,4)$,点 $B$ 的坐标为 $(-2,0)$,点 $C$ 的坐标为 $(3,0)$.
(1)求证：$\triangle ABC$ 是等腰三角形；
(2)若点 $P$ 在 $AO$ 上且点 $P$ 到 $\angle ACB$ 两边的距离相等,利用尺规作图,找出点 $P$ 的位置(保留作图痕迹),并求出 $\triangle ACP$ 的面积；
(3)若动点 $Q$ 从点 $O$ 出发,沿着 $O\to A\to C$ 的路径运动,当 $\triangle COQ$ 是等腰三角形时,直接写出点 $Q$ 的坐标.

答案：

(1)$\because A(0,4),B(-2,0),C(3,0)$，
$\therefore BC=|-2 - 3|=5,OA=4,OC=3$，
$\therefore AC=\sqrt{OA^2+OC^2}=\sqrt{4^2+3^2}=5$，
$\therefore AC=BC,\therefore \triangle ABC$为等腰三角形.
(2)如图1，点$P$的位置即为所求.
过点$P$作$PD\perp AC$于点$D$.
又$\because PO\perp BC,\therefore PO=PD$.
在$Rt\triangle PCD$和$Rt\triangle PCO$中，$\begin{cases}PO=PD\\PC=PC\end{cases}$
$\therefore Rt\triangle PCD\congRt\triangle PCO(HL)$，
$\therefore CD=OC=3,\therefore AD=AC - CD=2$.
设$PO=PD=x$，则$AP=4 - x$.
在$Rt\triangle APD$中，由勾股定理，得$AP^2=AD^2+DP^2$，
$\therefore (4 - x)^2=x^2+2^2$，解得$x=\frac{3}{2}$，
$\therefore S_{\triangle ACP}=\frac{1}{2}AC\cdot DP=\frac{1}{2}×5×\frac{3}{2}=\frac{15}{4}$.

(3)由题意，分以下四种情况讨论:
①当$OQ=OC=3$，且点$Q$在$AO$上时，如图2所示，
此时点$Q$的坐标为$(0,3)$；
②当$OQ=OC=3$，且点$Q$在$AC$上时，如图3所示，
过点$Q$作$QH\perp AO$于点$H$，过点$O$作$OD\perp AC$于点$D$.
$\because S_{\triangle AOC}=\frac{1}{2}AC\cdot OD=\frac{1}{2}OC\cdot OA$，
$\therefore OD=\frac{OA\cdot OC}{AC}=\frac{4×3}{5}=\frac{12}{5}$，
$\therefore CD=\sqrt{OC^2-OD^2}=\sqrt{3^2-(\frac{12}{5})^2}=\frac{9}{5}$.
$\because OQ=OC,OD\perp AC,\therefore CD=DQ=\frac{9}{5}$，
$\therefore AQ=AC - DQ - CD=\frac{7}{5}$.
$\because S_{\triangle AOQ}=\frac{1}{2}AQ\cdot OD=\frac{1}{2}AO\cdot HQ$，
$\therefore HQ=\frac{AQ\cdot OD}{OA}=\frac{\frac{7}{5}×\frac{12}{5}}{4}=\frac{21}{25}$，
$\therefore OH=\sqrt{OQ^2-HQ^2}=\sqrt{3^2-(\frac{21}{25})^2}=\frac{72}{25}$，
$\therefore$此时点$Q$的坐标为$(\frac{21}{25},\frac{72}{25})$；
③当$OQ=CQ$时，如图4所示，
过点$Q$作$DQ\perp OC$于点$D$，
则$CD=OD=\frac{1}{2}OC=\frac{3}{2},\angle QCO=\angle QOC$.
又$\because \angle OAQ+\angle QCO=\angle AOQ+\angle CQO=90°$，
$\therefore \angle OAQ=\angle AOQ,\therefore AQ=OQ,\therefore CQ=AQ=\frac{1}{2}AC=\frac{5}{2}$.
$\therefore QD=\sqrt{CQ^2-CD^2}=\sqrt{(\frac{5}{2})^2-(\frac{3}{2})^2}=2$，
$\therefore$此时点$Q$的坐标为$(\frac{3}{2},2)$；
④当$CQ=CO=3$时，如图5所示，
过点$Q$作$QM\perp OA$于点$M$，$QN\perp OC$于点$N$，过点$O$作$OD\perp AC$于点$D$，
则易得$OD=\frac{12}{5}$，$AQ=AC - CQ=2$.
$\because S_{\triangle AOQ}=\frac{1}{2}AQ\cdot OD=\frac{1}{2}AO\cdot QM$，
$\therefore QM=\frac{AQ\cdot OD}{AO}=\frac{2×\frac{12}{5}}{4}=\frac{6}{5}$.
$\because S_{\triangle COQ}=\frac{1}{2}CQ\cdot OD=\frac{1}{2}OC\cdot NQ$，
$\therefore QN=\frac{CQ\cdot OD}{OC}=\frac{3×\frac{12}{5}}{3}=\frac{12}{5}$，
$\therefore$此时点$Q$的坐标为$(\frac{6}{5},\frac{12}{5})$.
综上可知，点$Q$的坐标为$(0,3)$或$(\frac{21}{25},\frac{72}{25})$或$(\frac{3}{2},2)$或$(\frac{6}{5},\frac{12}{5})$.
　　　　　　

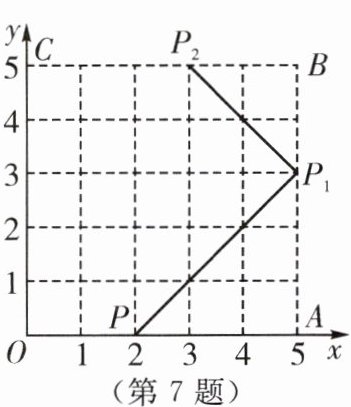
7. (2024·兴化市期末)如图,弹性小球从 $P(2,0)$ 出发,沿所示方向运动,每当小球碰到正方形 $OABC$ 的边时反弹,反弹时反射角等于入射角,当小球第一次碰到正方形的边时的点为 $P_1$,第二次碰到正方形的边时的点为 $P_2$,…,第 $n$ 次碰到正方形的边时的点为 $P_n$,则 $P_{2024}$ 的坐标是(2,0)

A.$(5,3)$
B.$(3,5)$
C.$(2,0)$
D.$(0,2)$

答案： C 解析:由题意，得:点$P_1$的坐标为$(5,3)$，点$P_2$的坐标为$(3,5)$，点$P_3$的坐标为$(0,2)$，点$P_4$的坐标为$(2,0)$，点$P_5$的坐标为$(5,3)\cdots\cdots\because 2024÷4=506,\therefore$点$P_{2024}$的坐标为$(2,0)$.

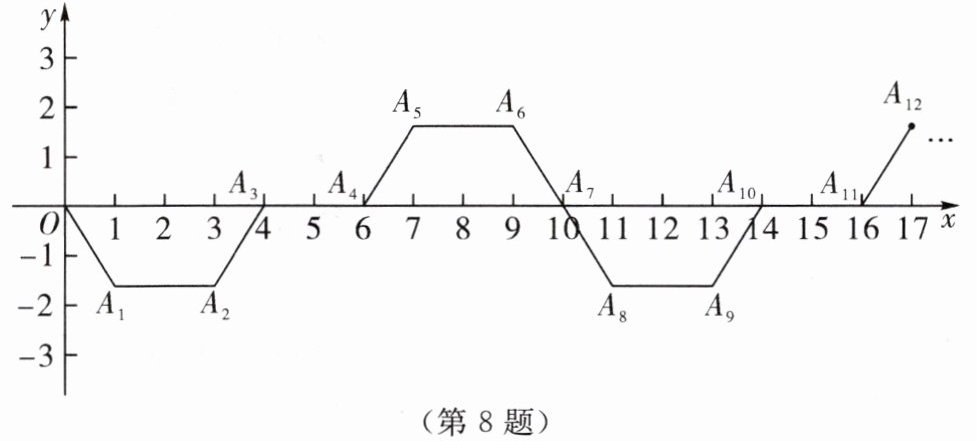
8. (2024·绥化)如图,已知 $A_1(1,-\sqrt{3})$,$A_2(3,-\sqrt{3})$,$A_3(4,0)$,$A_4(6,0)$,$A_5(7,\sqrt{3})$,$A_6(9,\sqrt{3})$,$A_7(10,0)$,$A_8(11,-\sqrt{3})$,…,依此规律,则点 $A_{2024}$ 的坐标为______(2891,-√3).

答案： $(2891,-\sqrt{3})$ 解析:由题意，得:点$A_1$的坐标为$(1,-\sqrt{3})$，点$A_2$的坐标为$(3,-\sqrt{3})$，点$A_3$的坐标为$(4,0)$，点$A_4$的坐标为$(6,0)$，点$A_5$的坐标为$(7,\sqrt{3})$，点$A_6$的坐标为$(9,\sqrt{3})$，点$A_7$的坐标为$(10,0)$，点$A_8$的坐标为$(11,-\sqrt{3})$，点$A_9$的坐标为$(13,-\sqrt{3})$，点$A_{10}$的坐标为$(14,0)$，点$A_{11}$的坐标为$(16,0)$，点$A_{12}$的坐标为$(17,\sqrt{3})$，点$A_{13}$的坐标为$(19,\sqrt{3})$，点$A_{14}$的坐标为$(20,0)$，$\cdots$，由此可见，每隔七个点，点$A_n$的横坐标增加10，且纵坐标按$-\sqrt{3}$，$-\sqrt{3},0,0,\sqrt{3},\sqrt{3},0$循环出现.又$\because 2024÷7=289\cdots\cdots1,\therefore 1+289×10=2891,\therefore$点$A_{2024}$的坐标为$(2891,-\sqrt{3})$.

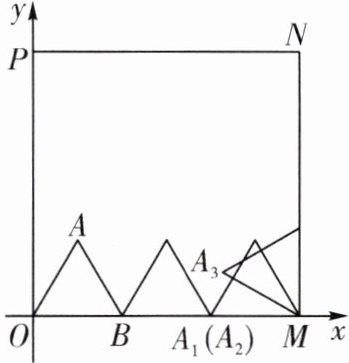
9. (2024·黑龙江改编)如图,在平面直角坐标系中,正方形 $OMNP$ 顶点 $M$ 的坐标为 $(6,0)$,$\triangle OAB$ 是等边三角形,点 $B$ 的坐标是 $(2,0)$,$\triangle OAB$ 在正方形 $OMNP$ 内部紧靠正方形 $OMNP$ 的边(方向为 $O\to M\to N\to P\to O\to M…\to$)做无滑动滚动,第一次滚动后,点 $A$ 的对应点记为 $A_1$,$A_1$ 的坐标是 $(4,0)$；第二次滚动后,$A_1$ 的对应点记为 $A_2$,$A_2$ 的坐标是 $(4,0)$；第三次滚动后,$A_2$ 的对应点记为 $A_3$,$A_3$ 的坐标是______,如此下去,…,则 $A_{2024}$ 的坐标是______.

$(6-\sqrt{3},1)$$(2,6)$

答案： $(6-\sqrt{3},1)$ $(2,6)$ 解析:由题意，得:点$A_1$的坐标是$(4,0)$，点$A_2$的坐标是$(4,0)$，点$A_3$的坐标是$(6-\sqrt{3},1)$，点$A_4$的坐标是$(6,4)$，点$A_5$的坐标是$(6,4)$，点$A_6$的坐标是$(5,6-\sqrt{3})$，点$A_7$的坐标是$(2,6)$，点$A_8$的坐标是$(2,6)$，点$A_9$的坐标是$(\sqrt{3},5)$，点$A_{10}$的坐标是$(0,4)$，点$A_{11}$的坐标是$(0,4)$，点$A_{12}$的坐标是$(1,\sqrt{3})$，点$A_{13}$的坐标是$(4,0)$，$\cdots$，由此可见，点$A_n$的坐标每12个循环一次.又$\because 2024÷12=168\cdots\cdots8,\therefore$点$A_{2024}$的坐标为$(2,6)$.