《2025年课时训练八年级数学上册人教版江苏人民出版社》

8 (2025·江西南昌期末)计算:
(1)$(x-1)(x^{2}+x+1);$
(2)$(x+3)(x-2)-x(x-1).$

答案：
(1)原式$=x^{3}+x^{2}+x-x^{2}-x-1$
$=x^{3}+x^{2}-x^{2}+x-x-1=x^{3}-1$.
(2)原式$=x^{2}-2x+3x-6-x^{2}+x$
$=x^{2}-x^{2}-2x+x+3x-6=2x-6$.

9 (2024·遂宁中考)下列运算结果正确的是( ).

A.$3a-2a= 1$
B.$a^{2}\cdot a^{3}= a^{6}$
C.$(-a)^{4}= -a^{4}$
D.$(a+3)(a-3)= a^{2}-9$

答案： D

10 (2025·湖北武汉九校联考月考)$(x-3)^{2}+(x-5)^{2}= 20$,则代数式$(x-4)^{2}= $( ).

A.8
B.9
C.10
D.11

答案： B

11 (2025·广东阳江城区期末)如图,小明利用4张图(1)所示的长为a,宽为b的长方形卡片,拼成图(2)所示的图形,则根据图(2)的面积关系能验证的恒等式为( ).


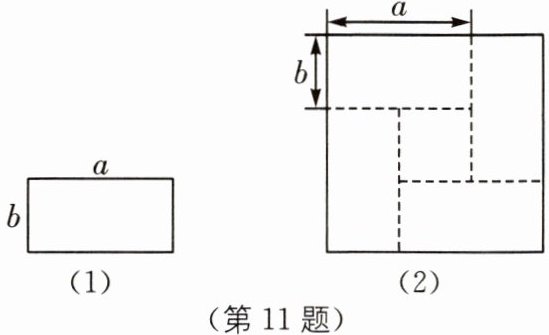
A.$(a+2b)^{2}= a^{2}+4ab+4b^{2}$
B.$(a+b)^{2}= (a-b)^{2}+4ab$
C.$(2a+b)^{2}= 4a^{2}+4ab+b^{2}$
D.$(a-b)^{2}= a^{2}-2ab+b^{2}$

答案： B

12 (2024·无锡中考)计算:$a(a-2b)+(a+b)^{2}.$

答案： 原式$=a^{2}-2ab+a^{2}+2ab+b^{2}=2a^{2}+b^{2}$.

13 (2025·安徽合肥庐江期末)计算:
$(3a+2b)^{2}+2b(a-2b).$

答案： 原式$=9a^{2}+12ab+4b^{2}+2ab-4b^{2}=9a^{2}+14ab$.

14 (2025·湖南长沙长郡中学期末)先化简,再求值:
$(x+2)^{2}+(x+2)(x-2)+2x(1-x)$,其中$x= \frac {1}{2}.$

答案： 原式$=x^{2}+4x+4+x^{2}-4+2x-2x^{2}=6x$.
当$x=\frac {1}{2}$时,原式$=6×\frac {1}{2}=3$.

15 (2025·天津西青区期末)一个长方体的长、宽、高分别是$2a,a^{2},(3a+1)$,这个长方体的体积是( ).

A.$6a^{2}+2$
B.$6a^{3}+2a$
C.$6a^{4}+2a^{2}$
D.$6a^{4}+2a^{3}$

答案： D

16 (2025·江西赣州南康十中期末)(1)已知$2x+5y-3= 0$,求$4^{x}\cdot 32^{y}$的值;
(2)若多项式$ax^{2}+bx+1与2x^{2}-3x+1的积不含x^{3}$项和x项,求a和b的值.

答案：
(1)$\because 2x+5y-3=0,\therefore 2x+5y=3$,
$\therefore 4^{x}\cdot 32^{y}=(2^{2})^{x}\cdot (2^{5})^{y}=2^{2x}\cdot 2^{5y}=2^{2x+5y}=2^{3}=8$.
(2)$(ax^{2}+bx+1)(2x^{2}-3x+1)$
$=2ax^{4}-3ax^{3}+ax^{2}+bx^{3}-3bx^{2}+bx+2x^{2}-3x+1$
$=2ax^{4}+(2b-3a)x^{3}+(a-3b+2)x^{2}+(b-3)x+1$.
由题意,得$\left\{\begin{array}{l} 2b-3a=0,\\ b-3=0,\end{array}\right. $解得$\left\{\begin{array}{l} a=2,\\ b=3,\end{array}\right. $
即a的值为2,b的值为3.

17 (2025·湖南长沙浏阳期末改编)如图,某小区有一块长为$(3a+b)$米,宽为$(2a+b)$米的长方形地块,开发商计划将阴影部分进行绿化,中间将修建一座雕像.
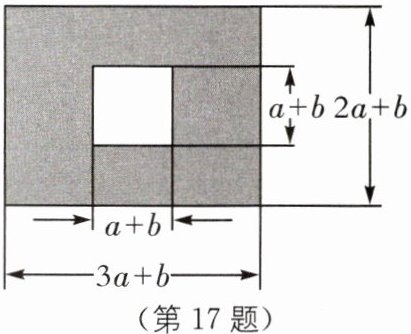
(1)用含有a,b的式子表示绿化的总面积;(结果写成最简形式)
(2)若$a= 8,b= \frac {5}{6}$,求出此时绿化的总面积.

答案：
(1)总面积为$(3a+b)(2a+b)-(a+b)^{2}=(5a^{2}+3ab)$平方米.
(2)将$a=8,b=\frac {5}{6}$代入,$5a^{2}+3ab=5×8^{2}+3×8×\frac {5}{6}=$
$320+20=340$(平方米).
故绿化的总面积为340平方米.