《2025年课时训练八年级数学上册人教版江苏人民出版社》

1 教材 P114探究·变式 (2024·上海宝山区期末)下列算式中,可用完全平方公式计算的是( ).

A.(1+x)(1-x)
B.(-x-1)(-1+x)
C.(x-1)(1+x)
D.(-x+1)(1-x)

答案： D

2 教材 P114探究·变式 (2025·湖南长沙期末)已知$(x-3)^2= x^2+mx+9,$则m的值为______.

答案： -6

3 教材 P115思考·变式 如图是利用割补法求图形面积的示意图,下列公式中与之相对应的是( ).

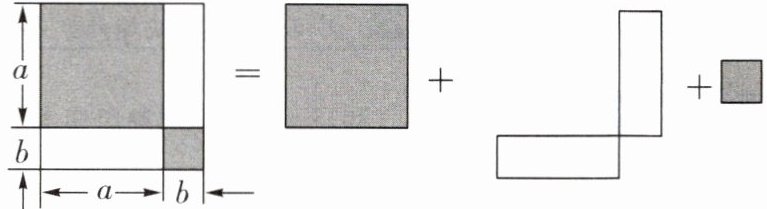
$A. (a+b)^2= a^2+2ab+b^2$
$B. (a-b)^2= a^2-2ab+b^2$
$C. (a+b)(a-b)= a^2-b^2$
$D. (ab)^2= a^2b^2$

答案： A

4 教材 P115例3·变式 (2025·河南周口太康期中)计算$(-x+2)^2$的结果是( ).
$A. x^2-4x+4$
$B. -x^2-4x+4$
$C. x^2+4x+4$
$D. -x^2+4x+4$

答案： A

5 教材 P115例3·变式 (2024·四川成都成华区期中)利用公式计算$(-x-2y)^2$的结果为( ).
$A. -x^2-2xy-4y^2$
$B. -x^2-4xy-4y^2$
$C. x^2-4xy+4y^2$
$D. x^2+4xy+4y^2$

答案： D

6 教材 P115例4·变式 运用完全平方公式计算：
(1)(2025·广东佛山君兰中学期中$)205^2；$
(2)(2025·上海实验学校附属东滩学校期中$)99.7^2.$

答案： 6.
(1)原式=(200+5)²=200²+2×200×5+5²=42025；
(2)原式=(100-0.3)²=100²-2×100×0.3+0.3²=10000-60+0.09=9940.09.

7 教材 P117练习 T1·变式 (2025·四川眉山期末)对多项式3a+4b-c进行添括号正确的是( ).

A.3a+(4b+c)
B.3a-(4b+c)
C.3a+4(b-c)
D.3a+(4b-c)

答案： D

8 教材 P116例5·变式 计算：
$(1)(-a+b+c)^2；$
$(2)(x-2y-3z)^2.$

答案： 8.
(1)原式=[(-a+b)+c]²=(-a+b)²+2(-a+b)c+c²=a²-2ab+b²-2ac+2bc+c²=a²+b²+c²-2ab+2bc-2ac；
(2)原式=[(x-2y)-3z]²=(x-2y)²-6z(x-2y)+9z²=x²-4xy+4y²-6xz+12yz+9z².

9 (2025·安徽合肥巢湖期末)已知$a^2+b^2= 16,$且1/2ab= -3,则a+b的值是( ).

A.4
B.±4
C.2
D.±2

答案： 9.D [解析]
∵a²+b²=16,且$\frac{1}{2}ab=-3$,
∴ab=-6,
∴(a+b)²=a²+2ab+b²=16-12=4,则a+b=±2.故选D.

10 (2025·福建福州平潭一中期中)若a+b= -4,ab= 2,则$a^2+b^2= ( ).$

A.11
B.12
C.-11
D.-12

答案： 10.B [解析]
∵a+b=-4,ab=2,
∴a²+b²=(a+b)²-2ab=(-4)²-2×2=12.故选B.

11 (2025·湖南师大附中博才实验学校期末)已知$a^2+b^2= 8,(a+b)^2= 20,$则ab= ______.

答案： 11.6 [解析]
∵(a+b)²=a²+2ab+b²=20,且a²+b²=8,
∴2ab+8=20,
∴ab=6.

12 (2025·湖南长沙期末)若a,b满足$(a+b)^2= 15,(a-b)^2= 3,$则4ab= ______.

答案： 12.12 [解析]由已知,可得(a+b)²=15,(a-b)²=3,则a²+b²+2ab=15①,a²+b²-2ab=3②,①-②,得4ab=15-3=12.故4ab=12.

13 换元法 (2025·福建泉州六中期中)已知$(x-2021)^2+(x-2025)^2= 34,$则$(x-2023)^2$的值是______.

答案： 13.13 [解析]设t=x-2023.
∵(x-2021)²+(x-2025)²=34,
∴(t+2)²+(t-2)²=34,即2t²+8=34,解得t²=13,即(x-2023)²的值为13.