《2025年课时训练八年级数学上册人教版江苏人民出版社》

1(2025·河南开封期末)如图,∠CBE和∠BCF是△ABC的两个外角,若∠A= 54°,则∠CBE+∠BCF的度数为______.

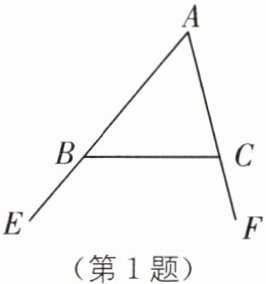
答案： 234° [解析] 由 A 字型问题的结论，得∠CBE+∠BCF=180°+∠A=180°+54°=234°.
一题多解
∵∠A=54°，
∴∠ABC+∠ACB=180°-54°=126°.
∵∠CBE 和∠BCF 是△ABC 的两个外角，
∴∠CBE+∠BCF=180°-∠ABC+180°-∠ACB=360°-126°=234°.

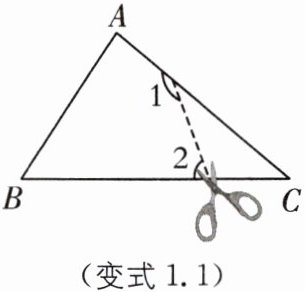
变式1.1(2025·重庆第十一中学校期中改编)如图,在△ABC中,∠C= 40°,按图中虚线将∠C剪去后,∠1+∠2等于______°.

答案： 220 [解析] 由 A 字模型的结论，得∠1+∠2=180°+∠C=180°+40°=220°.
一题多解
∵∠C=40°，
∴∠A+∠B=180°-∠C=140°，
∴∠1+∠2=360°-(∠A+∠B)=360°-140°=220°.

2(2025·江苏泰州期中)如图,在△ABC中,D在BC的延长线上,过点D作DF⊥AB于点F,交AC于点E.已知∠A= 32°,∠ECD= 85°,则∠D的度数为( ).

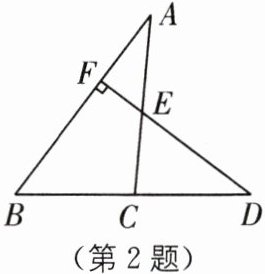
A.53°
B.37°
C.47°
D.38°

答案： B [解析]
∵DF⊥AB，
∴∠EFA=90°.△AEF 和△CDE 构成 8 字模型，根据 8 字模型的结论，得∠A+∠EFA=∠D+∠ECD.
∵∠A=32°，∠ECD=85°，
∴∠D=32°+90°-85°=37°.故选 B.
一题多解
∵DF⊥AB，
∴∠EFA=90°.在△AEF 中，∠EFA=90°，∠A=32°，
∴∠AEF=180°-∠EFA-∠A=180°-90°-32°=58°.
∵∠CED=∠AEF，
∴∠CED=58°.在△CDE 中，∠CED=58°，∠ECD=85°，
∴∠D=180°-∠CED-∠ECD=180°-58°-85°=37°.故选 B.

变式2.1(2025·海口龙华区一模)如图,∠C= ∠A= 90°,∠B= 25°,则∠D的度数是( ).

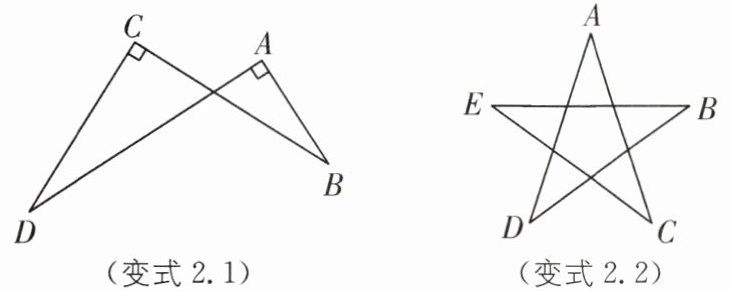
A.55°
B.35°
C.25°
D.20°

答案： C [解析] 线段 AD 和 BC 构成 8 字模型，根据 8 字模型的结论，得∠A+∠B=∠C+∠D.
∵∠C=∠A=90°，∠B=25°，
∴∠D=∠B=25°.故选 C.

变式2.2 如图,∠A+∠B+∠C+∠D+∠E的度数为( ).

A.90°
B.180°
C.120°
D.360°

答案： B [解析] 如图，连接 DC，根据“8 字形”数量关系，得∠B+∠E=∠1+∠2，
∴∠A+∠B+∠ACE+∠ADB+∠E=∠ADC+∠ACD+∠A=180°.故选 B.

3(2025·浙江舟山期中)如图,点E在BC上,ED⊥AC于点F,交BA的延长线于点D,已知∠D= 30°,∠C= 20°,则∠B的度数是______.

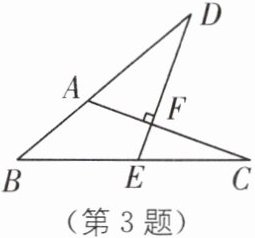
答案： 40° [解析]
∵ED⊥AC，
∴∠DFC=90°.
∵题图中∠B，∠C，∠D，∠DFC 构成燕尾模型中的四个角，
∴∠DFC=∠B+∠C+∠D，
∴∠B=∠DFC-∠C-∠D=90°-20°-30°=40°.

变式3.1 如图是一个零件示意图,经测量,得知∠A= 17°,∠B= 90°,∠D= 130°25',则∠C的度数为( ).


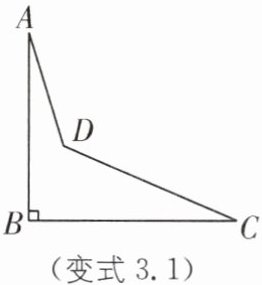
A.23°25'
B.33°
C.27°
D.23°

答案： A [解析] 所给图形构成燕尾模型，由燕尾模型的结论，得∠ADC=∠A+∠ABC+∠C，即130°25'=17°+90°+∠C，
∴∠C=23°25'.故选 A.