第50页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
9 一张正方形纸片经过两次对折,并在如图位置上剪去一个小正方形,打开后是( ).

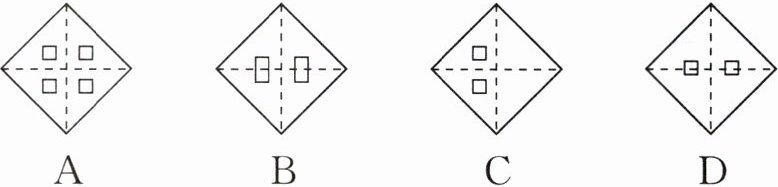


答案:
B
10 如图,在△ABC 中,点 D 在 BC 上,分别以 AB,AC 为对称轴,作点 D 的对称点 E,F,连接 AE,AF,根据图中标示的角度,求∠EAF 的度数.


答案:
连接AD.
∵点E,F分别是点D以AB,AC为对称轴的对称点,
∴∠EAB=∠DAB,∠FAC=∠DAC.在△ABC中,
∵∠BAC+∠B+∠C=180°,∠B=62°,∠C=51°,
∴∠BAC=67°,即∠DAB+∠DAC=67°,
∴∠EAF=∠EAB+∠DAB+∠DAC+∠FAC=134°.
∵点E,F分别是点D以AB,AC为对称轴的对称点,
∴∠EAB=∠DAB,∠FAC=∠DAC.在△ABC中,
∵∠BAC+∠B+∠C=180°,∠B=62°,∠C=51°,
∴∠BAC=67°,即∠DAB+∠DAC=67°,
∴∠EAF=∠EAB+∠DAB+∠DAC+∠FAC=134°.
11 (2025·河南南阳新野期末)如图,△ABC 和△ADE 关于直线 MN 对称,BC 和 DE 的交点 F 在直线 MN 上.
(1)若 ED= 15,BF= 9,求 EF 的长;
(2)若∠ABC= 35°,∠AED= 65°,∠BAE= 16°,求∠BFN 的度数;
(3)连接 BD 和 EC,判断 BD 和 EC 的位置关系,并说明理由.
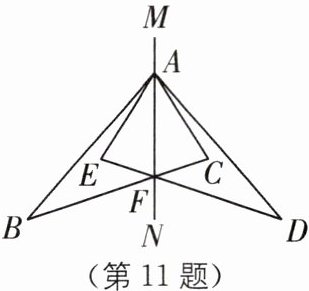
(1)若 ED= 15,BF= 9,求 EF 的长;
(2)若∠ABC= 35°,∠AED= 65°,∠BAE= 16°,求∠BFN 的度数;
(3)连接 BD 和 EC,判断 BD 和 EC 的位置关系,并说明理由.

答案:
(1)
∵△ABC和△ADE关于直线MN对称,ED=15,BF=9,
∴EF=CF,BF=DF=9,ED=CB=15,
∴EF=ED−DF=ED−BF=15−9=6.
(2)
∵△ABC和△ADE关于直线MN对称,∠ABC=35°,∠AED=65°,∠BAE=16°,
∴∠AED=∠ACB=65°,
∴∠BAC=180°−∠ABC−∠ACB=80°.
∵∠BAE=16°,
∴∠EAC=∠BAC−∠BAE=64°.
∵线段AE与AC关于直线MN对称,
∴∠EAN=∠CAN=$\frac{1}{2}$∠EAC=$\frac{1}{2}$×64°=32°,
∴∠BAN=∠BAE+∠EAN=16°+32°=48°,
∴∠BFN=∠ABC+∠BAN=35°+48°=83°.
(3)BD//EC.理由如下:由对称得MN⊥EC,MN⊥BD,
∴EC//BD.
(1)
∵△ABC和△ADE关于直线MN对称,ED=15,BF=9,
∴EF=CF,BF=DF=9,ED=CB=15,
∴EF=ED−DF=ED−BF=15−9=6.
(2)
∵△ABC和△ADE关于直线MN对称,∠ABC=35°,∠AED=65°,∠BAE=16°,
∴∠AED=∠ACB=65°,
∴∠BAC=180°−∠ABC−∠ACB=80°.
∵∠BAE=16°,
∴∠EAC=∠BAC−∠BAE=64°.
∵线段AE与AC关于直线MN对称,
∴∠EAN=∠CAN=$\frac{1}{2}$∠EAC=$\frac{1}{2}$×64°=32°,
∴∠BAN=∠BAE+∠EAN=16°+32°=48°,
∴∠BFN=∠ABC+∠BAN=35°+48°=83°.
(3)BD//EC.理由如下:由对称得MN⊥EC,MN⊥BD,
∴EC//BD.
12 中考新考法 操作探究 [定义]如图(1),OM 平分∠AOB,则称射线 OB,OA 关于 OM 对称.
[理解题意]
(1)如图(1),射线 OB,OA 关于 OM 对称且∠AOB= 45°,则∠AOM= ______度;
[应用实际]
(2)如图(2),若∠AOB= 45°,OP 在∠AOB 内部$,OP,OP_1 $关于 OB 对称$,OP,OP_2 $关于 OA 对称,求$∠P_1OP_2 $的度数;
(3)如图(3),若∠AOB= 45°,OP 在∠AOB 外部,且$ 0°<∠AOP<45°,OP,OP_1 $关于 OB 对称$,OP,OP_2 $关于 OA 对称,求$∠P_1OP_2 $的度数;
[拓展提升]
(4)如图(4),若$∠AOB= 45°,OP,OP_1 $关于∠AOB 的 OB 边对称$,∠AOP_1= 4∠BOP_1,$求∠AOP 的度数(直接写出答案).
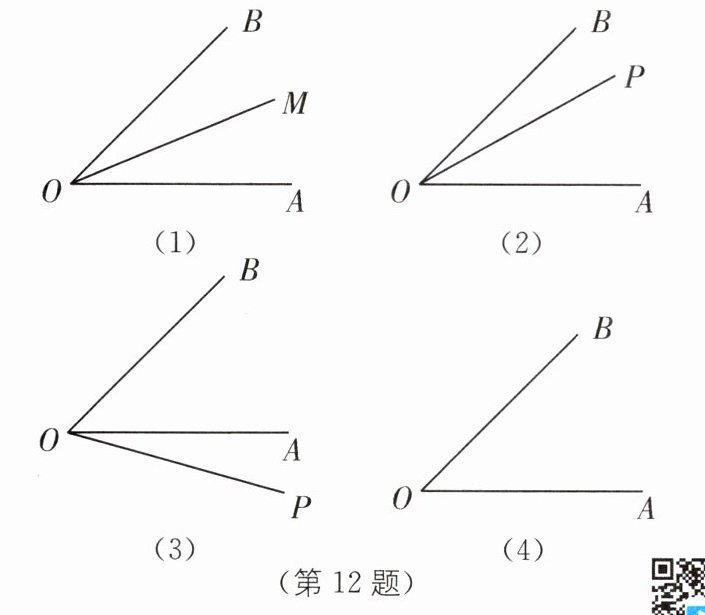
[理解题意]
(1)如图(1),射线 OB,OA 关于 OM 对称且∠AOB= 45°,则∠AOM= ______度;
[应用实际]
(2)如图(2),若∠AOB= 45°,OP 在∠AOB 内部$,OP,OP_1 $关于 OB 对称$,OP,OP_2 $关于 OA 对称,求$∠P_1OP_2 $的度数;
(3)如图(3),若∠AOB= 45°,OP 在∠AOB 外部,且$ 0°<∠AOP<45°,OP,OP_1 $关于 OB 对称$,OP,OP_2 $关于 OA 对称,求$∠P_1OP_2 $的度数;
[拓展提升]
(4)如图(4),若$∠AOB= 45°,OP,OP_1 $关于∠AOB 的 OB 边对称$,∠AOP_1= 4∠BOP_1,$求∠AOP 的度数(直接写出答案).

答案:
(1)22.5
(2)
∵OP和OP₁关于OB对称,
∴∠POP₁=2∠BOP.又OP和OP₂关于OA对称,
∴∠POP₂=2∠AOP.
∵∠P₁OP₂=∠POP₁+∠POP₂,
∴∠P₁OP₂=2∠BOP+2∠AOP=2∠AOB=90°.
(3)
∵OP和OP₁关于OB对称,
∴∠POP₁=2∠BOP.又OP和OP₂关于OA对称,
∴∠POP₂=2∠AOP.
∵∠P₁OP₂=∠POP₁−∠POP₂,
∴∠P₁OP₂=2∠BOP−2∠AOP=2∠AOB=90°.
(4)①若OP在∠AOB内部,如图
(1).由于题干中并未说明OP的明确位置,因此此处需分①OP在∠AOB内部,②OP在∠AOB外部两种情况讨论.
∵OP,OP₁关于∠AOB的边OB对称,
∴∠BOP=∠BOP₁.
∵∠AOP₁=4∠BOP₁,
∴∠AOB=3∠BOP₁=45°.
∴∠BOP₁=15°.
∴∠BOP=∠BOP₁=15°.
∴∠AOP=30°;②若OP在∠AOB外部.
∵∠AOP₁=4∠BOP₁,
∴射线OP在射线OB的上面,如图
(2).
∵OP,OP₁关于∠AOB的边OB对称,
∴∠BOP=∠BOP₁.
∵∠AOP₁=4∠BOP₁,
∴∠AOB=∠BOP₁+∠AOP₁=5∠BOP₁=45°.
∴∠BOP₁=9°.
∴∠BOP=∠BOP₁=9°.
∴∠AOP=45°+9°=54°.综上所述,∠AOP=30°或54°.
(1)22.5
(2)
∵OP和OP₁关于OB对称,
∴∠POP₁=2∠BOP.又OP和OP₂关于OA对称,
∴∠POP₂=2∠AOP.
∵∠P₁OP₂=∠POP₁+∠POP₂,
∴∠P₁OP₂=2∠BOP+2∠AOP=2∠AOB=90°.
(3)
∵OP和OP₁关于OB对称,
∴∠POP₁=2∠BOP.又OP和OP₂关于OA对称,
∴∠POP₂=2∠AOP.
∵∠P₁OP₂=∠POP₁−∠POP₂,
∴∠P₁OP₂=2∠BOP−2∠AOP=2∠AOB=90°.
(4)①若OP在∠AOB内部,如图
(1).由于题干中并未说明OP的明确位置,因此此处需分①OP在∠AOB内部,②OP在∠AOB外部两种情况讨论.
∵OP,OP₁关于∠AOB的边OB对称,
∴∠BOP=∠BOP₁.
∵∠AOP₁=4∠BOP₁,
∴∠AOB=3∠BOP₁=45°.
∴∠BOP₁=15°.
∴∠BOP=∠BOP₁=15°.
∴∠AOP=30°;②若OP在∠AOB外部.
∵∠AOP₁=4∠BOP₁,
∴射线OP在射线OB的上面,如图
(2).
∵OP,OP₁关于∠AOB的边OB对称,
∴∠BOP=∠BOP₁.
∵∠AOP₁=4∠BOP₁,
∴∠AOB=∠BOP₁+∠AOP₁=5∠BOP₁=45°.
∴∠BOP₁=9°.
∴∠BOP=∠BOP₁=9°.
∴∠AOP=45°+9°=54°.综上所述,∠AOP=30°或54°.
查看更多完整答案,请扫码查看


