《2025年课时训练八年级数学上册人教版江苏人民出版社》

12 若分式$\frac{2(x-3)}{x^{2}+3}$的值为0,则$\frac{2x}{x^{2}-1} ÷ \frac{2x}{1-x}$的值为______.

答案： $-\frac{1}{4}$

13 教材P148练习T4·变式 甲、乙两个工程队合修一条公路,已知甲工程队每天修$(a^{2}-4)m$,乙工程队每天修$(a-2)^{2}m$(其中$a＞2$),则甲工程队修900 m所用时间是乙工程队修600 m所用时间的多少倍？

答案： 甲工程队修900 m所用时间为$\frac{900}{a^{2}-4}$天,乙工程队修600 m所用时间为$\frac{600}{(a-2)^{2}}$天,由题意可得$\frac{900}{a^{2}-4}÷ \frac{600}{(a-2)^{2}}=\frac{900}{(a+2)(a-2)}\cdot \frac{(a-2)^{2}}{600}=\frac{3a-6}{2a+4}$.$\therefore$甲工程队修900 m所用时间是乙工程队修600 m所用时间的$\frac{3a-6}{2a+4}$倍.

14 课堂上,李老师给大家出了这样一道题：当x为$3,\pi,\sqrt{3}$时,求式子$\frac{x^{2}-2x+1}{x^{2}-1} ÷ \frac{2x-2}{x+1}$的值. 小明一看,“太复杂了,怎么算呢？”你能帮小明解决这个问题吗？

答案： 原式$=\frac{(x-1)^{2}}{(x+1)(x-1)}\cdot \frac{x+1}{2(x-1)}=\frac{1}{2}$.故当$x=3,\pi,\sqrt{3}$时,式子的值都是$\frac{1}{2}$.

15 在学习了分式的乘除法之后,老师给出了这样一道题,计算：$(a+\frac{1}{a})(a^{2}+\frac{1}{a^{2}})(a^{4}+\frac{1}{a^{4}})(a^{8}+\frac{1}{a^{8}})(a^{2}-1)$,同学们都感到无从下手,小明将$a^{2}-1变形为a(a-\frac{1}{a})$,然后用平方差公式很轻松地得出结论.你知道他是怎么做的吗？

答案： $\left(a+\frac{1}{a}\right)\left(a^{2}+\frac{1}{a^{2}}\right)\left(a^{4}+\frac{1}{a^{4}}\right)\left(a^{8}+\frac{1}{a^{8}}\right)(a^{2}-1)$$=a\left(a-\frac{1}{a}\right)\left(a+\frac{1}{a}\right)\left(a^{2}+\frac{1}{a^{2}}\right)\left(a^{4}+\frac{1}{a^{4}}\right)\left(a^{8}+\frac{1}{a^{8}}\right)$$\to$凑出平方差公式的形式$=a\left(a^{2}-\frac{1}{a^{2}}\right)\left(a^{2}+\frac{1}{a^{2}}\right)\left(a^{4}+\frac{1}{a^{4}}\right)\left(a^{8}+\frac{1}{a^{8}}\right)$$=a\left(a^{4}-\frac{1}{a^{4}}\right)\left(a^{4}+\frac{1}{a^{4}}\right)\left(a^{8}+\frac{1}{a^{8}}\right)$$=a\left(a^{8}-\frac{1}{a^{8}}\right)\left(a^{8}+\frac{1}{a^{8}}\right)=a\left(a^{16}-\frac{1}{a^{16}}\right)=a^{17}-\frac{1}{a^{15}}$.

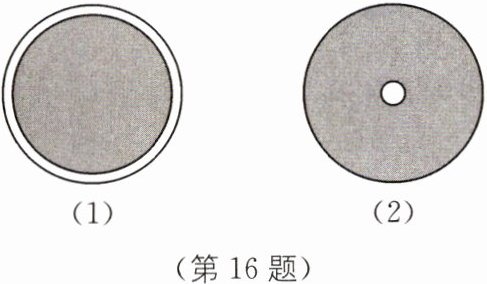
16 原创素养题 几何直观 如图(1)为“惠民1号”玉米试验田,是半径为R m的圆去掉宽为1 m的出水沟(空白部分)剩下的部分；如图(2)为“惠民2号”玉米试验田,是半径为R m的圆中间去掉半径为1 m的圆(空白部分)剩下的部分,两块玉米试验田的玉米都收了450 kg.
(1)哪块玉米试验田的玉米的单位面积产量高？
(2)两块玉米试验田的玉米单位面积产量高的是单位面积产量低的多少倍？

答案：
(1)“惠民1号”玉米试验田面积是$\pi(R-1)^{2}$米$^{2}$,单位面积产量是$\frac{450}{\pi(R-1)^{2}}$千克/米$^{2}$;“惠民2号”玉米试验田面积是$\pi(R^{2}-1^{2})$米$^{2}$,单位面积产量是$\frac{450}{\pi(R^{2}-1^{2})}$千克/米$^{2}$.$\because R^{2}-1-(R-1)^{2}=2(R-1),R-1＞0$,$\therefore 0＜(R-1)^{2}＜R^{2}-1$,$\therefore \frac{450}{\pi(R^{2}-1^{2})}＜\frac{450}{\pi(R-1)^{2}}$,$\therefore$“惠民1号”玉米的单位面积产量高.
(2)$\frac{450}{\pi(R-1)^{2}}÷ \frac{450}{\pi(R^{2}-1^{2})}=\frac{R+1}{R-1}$.故高的单位面积产量是低的单位面积产量的$\frac{R+1}{R-1}$倍.