《2025年课时训练八年级数学上册人教版江苏人民出版社》

1(2025·江西南昌二十八中期末改编)如图的两个三角形全等,则∠1的度数为 .
]

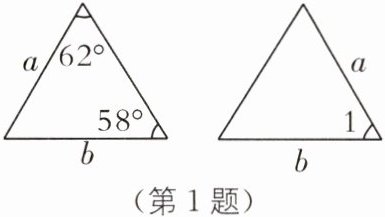
答案： 60°

2(2023·成都中考)如图,已知△ABC≌△DEF,点B,E,C,F依次在同一条直线上. 若BC= 8,CE= 5,则CF的长为 .
]

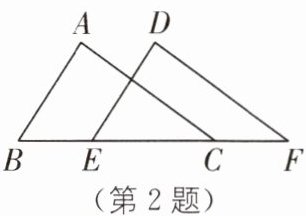
答案： 3

3 如图,将两块大小相同的直角三角板(∠B= ∠C= 30°)按图中所示的位置摆放. 若BE交CF于点D,交AC于点M,AB交CF于点N,则下列结论：①∠EAM= ∠FAN；②△ACN≌△ABM；③∠EAF+∠BAC= 120°；④EM= FN；⑤CF⊥BE,其中正确的结论有( ).

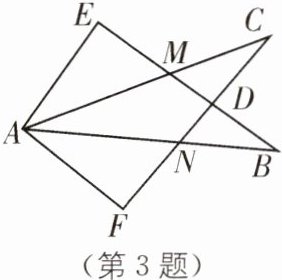
A.5个


B.4个
C.3个
D.2个
]

答案： B

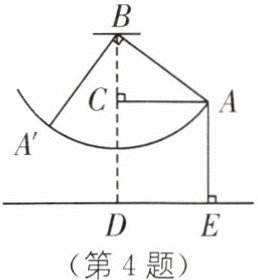
4 新情境 模拟海盗冒险场景 (2025·广东东莞南城开心实验学校期中)海盗船是一种模拟海盗冒险场景的游乐项目. 如图,当海盗船静止时,转轴B到地面的距离BD= 15 m. 当海盗船的船头在A处时,AC⊥BD,此时测得点A到地面的距离AE= 9 m. 当船头从A处摆动到A'处时,A'B⊥AB,则点A'到BD的距离为 .
]

答案： 6m

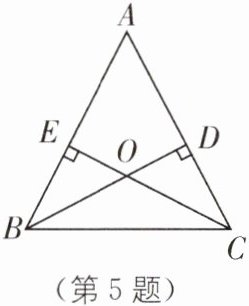
5 如图,在△ABC中,BD⊥AC,CE⊥AB,BD,CE交于点O,且BD= CE. 求证：∠DBC= ∠ECB.
]

答案：
∵CE⊥AB,BD⊥AC,
∴∠BEC=∠CDB=90°.在Rt△BCE与Rt△CBD中，{CE=BD,BC=CB,
∴Rt△BCE≌Rt△CBD(HL),
∴∠DBC=∠ECB.

6 中考新考法 满足结论的条件开放 (2024·淄博中考)如图,已知AB= CD,点E,F在线段BD上,且AF= CE.
请从①BF= DE；②∠BAF= ∠DCE；③AF= CF中. 选择一个合适的选项作为已知条件,使得△ABF≌△CDE.
你添加的条件是： (只填写一个序号).
添加条件后,请证明AE//CF.
]

答案： (答案不唯一)当选择①BF=DE时，证明如下:在△ABF和△CDE中，{AB=CD,AF=CE,BF=DE,
∴△ABF≌△CDE(SSS),
∴∠B=∠D.
∵BF=DE,
∴BF+EF=DE+EF,即BE=DF.在△ABE和△CDF中，{AB=CD,∠B=∠D,BE=DF,
∴△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴AE//CF；当选择②∠BAF=∠DCE时，证明如下:在△ABF和△CDE中，{AB=CD,∠BAF=∠DCE,AF=CE,
∴△ABF≌△CDE(SAS),
∴∠B=∠D,BF=DE,同理可证△ABE≌△CDF(SAS),
∴∠AEB=∠CFD,
∴AE//CF；当选择③AF=CF时，不能判定△ABF≌△CDE.