《2025年课时训练八年级数学上册人教版江苏人民出版社》

1 教材 P106 问题 2·变式 如图,根据图(1)的面积可以说明多项式的乘法运算 $(2a + b)(a + b) = 2a^2 + 3ab + b^2$,那么根据图(2)的面积可以说明多项式的乘法运算是( ).


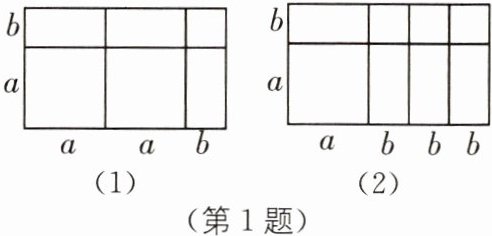
A.$(a + 3b)(a + b) = a^2 + 4ab + 3b^2$
B.$(a + 3b)(a + b) = a^2 + 3b^2$
C.$(b + 3a)(b + a) = b^2 + 4ab + 3a^2$
D.$(a + 3b)(a - b) = a^2 + 2ab - 3b^2$

答案： A

2 (2025·云南红河州期末)若 $(a + 3)·(a + 2b) = a^2 - 2a - 15$,则 b 等于( ).

A.5
B.$-\frac{5}{2}$
C.2
D.-2

答案： B

3 (2025·上海长宁区西延安中学期中)计算：$(x + 2y)·(-2x + 3y) = $______.

答案： $-2x^{2}-xy+6y^{2}$

4 教材 P107 例 3·变式 (2025·河南洛阳洛宁期末)计算：$(a - b)(a^2 + ab + b^2) = $______.

答案： $a^{3}-b^{3}$

5 教材 P107 例 3·变式 计算：
(1)(2025·重庆铜梁区巴川中学期中)$(4y + 1)(5 - y)$；
(2)(2025·上海新世纪中学期中)$(m + 2n)(2m - n)$.

答案：
(1)原式$=20y+5-4y^{2}-y=-4y^{2}+19y+5.$
(2)原式$=2m^{2}-mn+4mn-2n^{2}=2m^{2}+3mn-2n^{2}.$

6 教材 P107 练习 T2·拓展 (2024·广东清远阳山期末)计算下列各式,然后回答问题：
$(a + 5)(a + 2) = $______；$(a + 5)(a - 2) = $______；
$(a - 5)(a + 2) = $______；$(a - 5)(a - 2) = $______.
(1)从上面的计算中总结规律,用公式可表示为：$(x + p)(x + q) = $______；
(2)运用上面的规律,直接写出下式的结果：
①$(x + 10)(x - 23) = $______；
②$(x - 25)(x - 20) = $______；
(3)若 $(x + p)(x + q) = x^2 + kx + 18$ 成立,且 k,p,q 均为整数,则满足条件的 k 的值可以是______.

答案： $a^{2}+7a+10$ $a^{2}+3a-10$ $a^{2}-3a-10$ $a^{2}-7a+10$
(1)$x^{2}+(p+q)x+pq$
(2)①$x^{2}-13x-230$ ②$x^{2}-45x+500$
(3)$\pm 9,\pm 11,\pm 19$

7 教材 P111 习题 T10·变式 (2025·青海果洛州达日期末改编)为了更好地开展劳动教育,某学校暑期对学校闲置的地块进行规划改造,已知该地块如图是长为 $(a + 4b)$ 米,宽为 $(a + 3b)$ 米的长方形地块,学校准备在该地块内修一条平行四边形小路,小路的底边宽为 a 米,并计划将阴影部分改造为种植区. 用含有 a,b 的式子分别表示出小路面积 $S_1$ 和种植区的总面积 $S_2$.(请将结果化为最简)

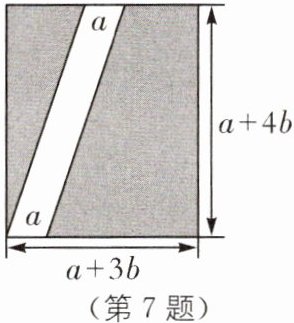
答案： $S_{1}=a(a+4b)=(a^{2}+4ab)$平方米，$S_{2}=(a+3b-a)(a+4b)=3b(a+4b)=(3ab+12b^{2})$平方米.$\to S_{2}=(a+3b)(a+4b)-S_{1}=(3ab+12b^{2})$平方米