《2025年课时训练八年级数学上册人教版江苏人民出版社》

10 已知$ x(x-3)= 2 $,那么多项式$ -2x^{2}+6x+9 $的值是( ).

A.4
B.5
C.6
D.7

答案： B

11 要使$ (x^{2}+ax+1)\cdot (-6x^{3}) 的展开式中不含 x^{4} $项,则 a 应等于( ).

A.6
B.-1
C.$ \frac{1}{6} $
D.0

答案： D

12 若$ A= 3x-2,B= 1-2x,C= -6x $,则$ C\cdot B+A\cdot C $= ______.

答案： -6x²+6x

13 若不论 x 为何值,等式$ x(2x+a)+4x-3b= 2x^{2}+5x+6 $恒成立,则 a,b 的值应分别是______.

答案： 1和-2

14 若$ ab^{2}= -1 $,求$ -ab(a^{2}b^{5}-ab^{3}-2b) $的值.

答案： 原式=-a³b⁶+a²b⁴+2ab²=(-ab²)³+(ab²)²+2(ab²)=1+1-2=0.

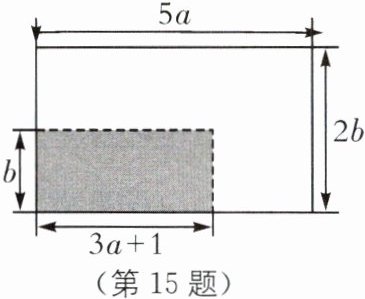
15 (2024·河北秦皇岛青龙期末)某居民小组在进行美丽乡村建设中,规划将一长为 5a 米,宽为 2b 米的长方形场地打造成居民健身场所,如图所示,具体规划为:在这个场地一角分割出一块长为$ (3a+1) $米,宽为 b米 的长方形场地建篮球场,其余的地方安装各种健身器材,其中用作篮球场 的地面铺设塑胶地面,用于安装健身器材的区域建水泥地面.
(1)用含 a,b 的式子表示篮球场地的面积$ S_{1} 和安装健身器材区域的地面面积 S_{2} $;
(2)当$ a= 9 $米,$ b= 15 $米时,分别求出篮球场地的面积 和安装健身器材区域的地面面积;
(3)在(2) 的条件下,如果铺设塑胶地面每平方米需100元,铺设水泥地面每平方米需50元,求建设该居民健身场所所需的地面总费用 M(元).

答案：
(1)S₁=b(3a+1)=3ab+b(平方米)，S₂=5a×2b-b(3a+1)=7ab-b(平方米).
(2)当a=9米,b=15米时，S₁=3×9×15+15=420(平方米)，S₂=7×9×15-15=930(平方米).
(3)M=420×100+930×50=88500(元).

16 中考新考法 规律探究 已知一些两位数相乘的算式:
$ 62× 11,78× 69,34× 11,63× 67,18× 22,15× 55,12× 34,54× 11 $.
利用这些算式探究两位数乘法中可以简化运算的特殊情形:
(1)观察已知算式,选出具有共同特征的 3 个算式,并用文字描述它们的共同特征.
(2)分别计算你选出的算式.观察计算的结果,你能发现不经过乘法运算就可以快速,直接地写出积的规律吗?请用文字描述这个规律.
(3)证明你发现的规律.
(4)在已知算式中,找出所有可以应用(或经过转化可以应用)上述规律的算式,并将它们写在横线上:______.

答案：
(1)62× 11,34× 11,54× 11.这3个算式的共同特征是:一个两位数与11相乘.
(2)62×11=682,34×11=374,54×11=594，规律:两位数乘法中,如果有一个因数为11,得数的百位上的数是两个因数最高位上的积,十位上的数是第一个因数各个位数的和(满10进1),个位上的数是两个因数个位上数的积.
(3)设一个两位数为10a+b,另一个数为11，则它们的积为(10a+b)·11=110a+11b=100a+10a+10b+b=100a+10(a+b)+b.
(4)18× 22 15× 55