《2025年课时训练八年级数学上册人教版江苏人民出版社》

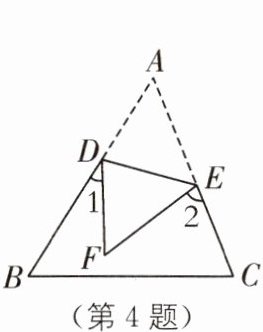
4(2025·重庆綦江区期中)如图,将三角形纸片ABC沿DE折叠,点A落在点F处,已知∠1+∠2= 100°,则∠A的度数为( ).

A.80°
B.100°
C.50°
D.以上都不对

答案： C [解析]
∵∠F 由∠A 折叠得到，
∴∠F=∠A，由风筝模型的结论，得∠1+∠2=∠A+∠F=2∠A=100°，
∴∠A=50°.故选 C.
一题多解 根据折叠的性质知，∠ADE=∠FDE，∠AED=∠FED.
∵∠1+∠FDE+∠ADE=180°，∠2+∠FED+∠AED=180°，
∴∠ADE+∠AED=$\frac{1}{2}$(180°-∠1+180°-∠2)=$\frac{1}{2}$×[360°-(∠1+∠2)]=$\frac{1}{2}$×(360°-100°)=130°.在△ADE 中，∠ADE+∠AED=130°，
∴∠A=180°-(∠ADE+∠AED)=180°-130°=50°.故选 C.

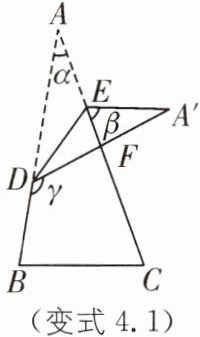
变式4.1(2025·浙江宁波期中)如图,将一张三角形纸片ABC的一角折叠,使点A落在△ABC外的A'处,折痕为DE.如果∠A= α,∠CEA'= β,∠BDA'= γ,那么下列式子中正确的是( ).

A.γ= 2α+β
B.γ= α+2β
C.γ= α+β
D.γ= 180°-α-β

答案： A [解析] 由折叠，得∠A=∠A'=α，由风筝模型的拓展结论特殊化，得γ-β=α+∠A'=2α，
∴γ=2α+β.故选 A.

5 如图,△ABC的角平分线BD,CE交于点O,若∠ACB= 80°,∠A= 60°,则∠BOE= ( ).

A.40°
B.50°
C.60°
D.55°

答案： C [解析]
∵△ABC 的角平分线 BD，CE 交于点 O，由双内角平分线模型的结论，得∠BOC=90°+$\frac{1}{2}$∠A=90°+$\frac{1}{2}$×60°=120°，
∴∠BOE=180°-∠BOC=180°-120°=60°.故选 C.

变式5.1 如图,△ABC的两个外角的平分线相交于点O,若∠A= 80°,则∠O等于( ).

A.40°
B.50°
C.60°
D.80°

答案： B [解析]
∵∠CBD，∠BCE 的平分线相交于点 O，由双外角平分线模型的结论，得∠O=90°-$\frac{1}{2}$∠A=90°-$\frac{1}{2}$×80°=50°.故选 B.

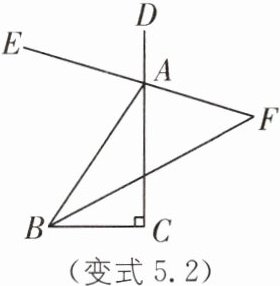
变式5.2 如图,在△ABC中,∠C= 90°,AE是△ABC的外角∠BAD的平分线,BF平分∠ABC与AE的反向延长线相交于点F,则∠BFE的度数为( ).


A.35°
B.40°
C.45°
D.50°

答案： C [解析] 如图，延长 BA 到点 G.
∵AE 是△ABC 的外角∠BAD 的平分线，
∴AF 是△ABC 的外角∠CAG 的平分线.
∵BF 平分∠ABC，
∴由内外角平分线模型的结论，得∠F=$\frac{1}{2}$∠C.
∵∠C=90°，
∴∠F=45°.故选 C.

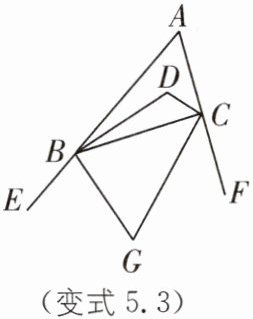
变式5.3 如图,在△ABC中,BD,CD分别平分∠ABC,∠ACB,BG,CG分别平分三角形的两个外角∠EBC,∠FCB,则∠D和∠G存在什么样的数量关系?

答案： ∠D+∠G=180°.理由如下：
∵BD，CD 分别平分∠ABC，∠ACB，
∴∠A，∠D 构成双内角平分线模型，
∴∠D=90°+$\frac{1}{2}$∠A.
∵BG，CG 分别平分三角形的两个外角∠EBC，∠FCB，
∴∠A，∠G 构成双外角平分线模型，
∴∠G=90°-$\frac{1}{2}$∠A，
∴∠D+∠G=90°+$\frac{1}{2}$∠A+90°-$\frac{1}{2}$∠A=180°.