《2025年课时训练八年级数学上册人教版江苏人民出版社》

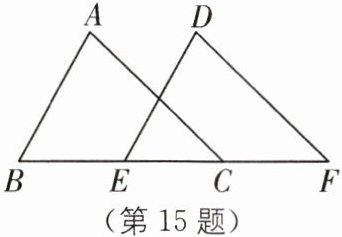
15(2025·广东佛山三水区期末)如图,已知点B,E,C,F在同一直线上,AB= DE,∠A= ∠D,AB//DE. 求证：
(1)△ABC≌△DEF；
(2)AC//DF.
]

答案：
(1)
∵AB//DE,
∴∠ABC=∠DEF.在△ABC和△DEF中，{∠A=∠D,AB=DE,∠ABC=∠DEF,
∴△ABC≌△DEF(ASA).
(2)
∵△ABC≌△DEF,
∴∠ACB=∠DFE,
∴AC//DF.

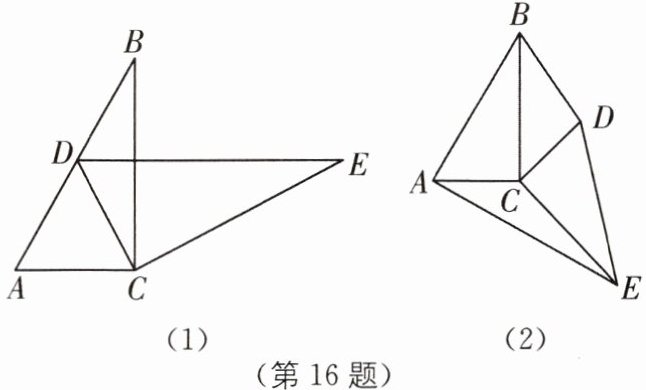
16 已知△ABC≌△DEC,∠ACB= 90°,∠B= 32°.
(1)如图(1),当点D在AB上,∠ACD= .
(2)如图(2),猜想△BDC与△ACE的面积有何关系？请说明理由.
]

答案：
(1)64°
(2)S△BDC=S△ACE.理由如下:如图,过点D作DF⊥BC于点F,过点A作AG⊥EC交EC的延长线于点G,
∴∠AGC=∠DFC=90°.
∵△ABC≌△DEC,
∴BC=EC,AC=DC.
∵∠ACG+∠GCB=90°,∠GCB+∠FCD=90°,
∴∠ACG=∠DCF.在△ACG和△DCF中，{∠AGC=∠DFC,∠ACG=∠DCF,AC=DC,
∴△ACG≌△DCF(AAS),
∴AG=DF.
∵S△BDC=$\frac{1}{2}$BC·DF,S△ACE=$\frac{1}{2}$·CE·AG,AG=DF,BC=EC,
∴S△BDC=S△ACE.

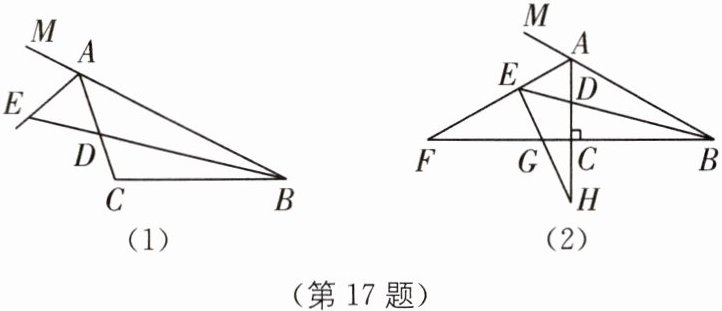
17(2024·宁夏中考改编)[综合与实践]
如图(1),在△ABC中,BD是∠ABC的平分线,BD的延长线交外角∠CAM的平分线于点E.
[发现结论]
结论1：∠AEB= ∠ACB；
结论2：当图(1)中∠ACB= 90°时,如图(2)所示,延长BC交AE于点F,过点E作AF的垂线交BF于点G,交AC的延长线于点H,则AE与EG的数量关系是 ；
[应用结论]求证：AH= GF.
]

答案： [发现结论]结论1：$\frac{1}{2}$　[解析]
∵BD是∠ABC的平分线，
∴∠ABC=2∠ABE.
∵AE是∠CAM的平分线，
∴∠CAM=2∠EAM.
∵∠CAM=∠ACB+∠ABC,
∴2∠EAM=∠ACB+2∠ABE.
∵∠EAM=∠AEB+∠ABE,
∴2(∠AEB+∠ABE)=∠ACB+2∠ABE,
∴∠AEB=$\frac{1}{2}$∠ACB.结论2：AE=EG　[解析]由结论1知,∠AEB=$\frac{1}{2}$∠ACB.
∵∠ACB=90°,
∴∠AED=$\frac{1}{2}$∠ACB=45°.
∵EH⊥AF,
∴∠AEH=90°,
∴∠AEB=∠BEG=45°.
∵∠ABE=∠GBE,BE=BE,
∴△ABE≌△GBE(ASA),
∴AE=EG.[应用结论]求证：AH=GF.在Rt△AFC中，∠EFG+∠EAH=90°,在Rt△AEH中，∠AHE+∠EAH=90°,
∴∠EFG=∠EHA.在△EFG和△EHA中，{∠EFG=∠EHA,∠FEG=∠HEA,EG=EA,
∴△EFG≌△EHA(AAS),
∴AH=GF.