《2025年课时训练八年级数学上册人教版江苏人民出版社》

1 教材 P105 问题·改编 观察图,有一边为 m 的三个长方形拼在一起,用不同的方法表示整个图形的面积可以说明下列哪个等式成立( ).

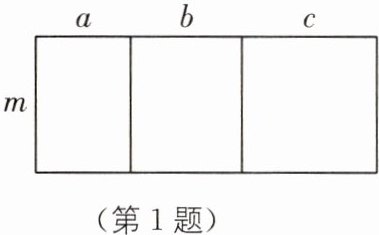
A.$ m(a+b+c)= ma+mb+mc $
B.$ (a+b)m= (b+c)m $
C.$ a(a+b+c)= a^{2}+ab+ac $
D.$ ma+mb+mc= a^{2}+b^{2}+c^{2} $

答案： A

2 (2024·福建泉州五中期中)通过计算几何图形的面积可表示一些代数恒等式(一定成立的等式),请根据图写出一个代数恒等式是______.

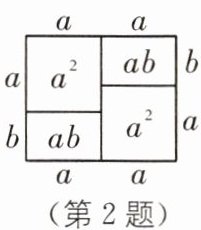
答案： 2a(a+b)=2a²+2ab

3 教材 P105 例 2·变式 (2025·江苏南通通州区期中)计算$ -3mn\left(m-\frac{1}{2}n\right) $的结果是( ).

A.$ 3m^{2}n+mn^{2} $
B.$ -3m^{2}n-\frac{3}{2}mn^{2} $
C.$ -3m^{2}n+\frac{3}{2}mn^{2} $
D.$ -3m^{2}n+\frac{1}{2}mn^{2} $

答案： C

4 (2024·甘肃白银期末改编)计算:$ (4a-b)\cdot (-2b)^{2} $= ______.

答案： 16ab²-4b³

5 计算:$ -m(3-m)+2(3-2m) $= ______.

答案： m²-7m+6

6 教材 P105 例 2·拓展 今天数学课上,老师讲了单项式乘多项式,放学回到家,小明拿出笔记复习,发现一道题:$ -3xy\cdot (4y-2x-1)= -12xy^{2}+6x^{2}y+□ $,□的地方被墨水弄污了,你认为□处应填写______.

答案： 3xy

7 教材 P105 例 1·拓展 计算:
(1)(2025·上海静安区田家炳中学期中)$ (a^{2}b+ab^{2}-3b^{3})\cdot (4ab^{2})-(-2ab^{2})^{2} $;
(2)(2024·江苏南通海门区东洲国际学校月考)$ x(2x-5)+3x(x+2)-5x(x-1) $.

答案：
(1)原式=a²b·(4ab²)+ab²·(4ab²)-3b³·(4ab²)-4a²b⁴=4a³b³+4a²b⁴-12ab⁵-4a²b⁴=4a³b³-12ab⁵.
(2)原式=2x²-5x+3x²+6x-5x²+5x=2x²+3x²-5x²+6x+5x-5x=6x.

8 教材 P111 习题 T10·变式 一个长方体的长、宽、高分别为$ 2x-1,2x,x^{2} $,则它的体积等于( ).

A.$ 4x^{4}-4x^{2} $
B.$ 4x^{4}-2x^{3} $
C.$ 4x^{3}-2x^{2} $
D.$ 4x^{4} $

答案： B

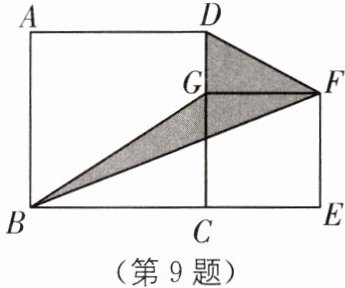
9 教材 P111 习题 T10·变式 有一个零件的形状如图所示(图中阴影部分),已知图中大正方形的边长为 a 米,小正方形的边长为 b 米.
(1)用含 a,b 的式子表示这个零件的面积.
(2)已知$ a= 1.2,b= 0.8 $,制作该零件的材料价格为 100 元/平方米,求制作一个该零件至少需要多少钱?

答案：
(1)这个零件的面积为$\frac{1}{2}b²+\frac{1}{2}(a-b)b=\frac{1}{2}ab$(平方米).
(2)当a=1.2,b=0.8时,制作一个该零件至少需要$\frac{1}{2}×1.2×0.8×100=48$(元).