第43页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
7 如图,直线 a,b,c 表示三条互相交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( ).
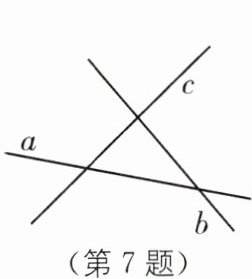
A.1 处
B.2 处
C.3 处
D.4 处

A.1 处
B.2 处
C.3 处
D.4 处
答案:
D
8 (2025·浙江长青教育发展共同体期末)如图,将△ABC 纸片沿 DE 折叠,点 A 落在点 A'处,恰好满足 A'B 平分∠ABC,A'C 平分∠ACB,若∠1= 125°,则∠2 的度数为______.
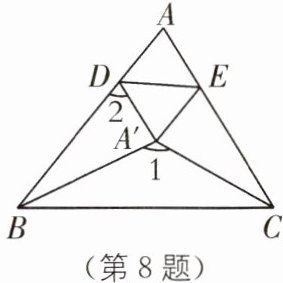

答案:
70° [解析]如图,连接AA',过A'作A'M⊥AB,A'N⊥BC,A'P⊥AC.
∵A'B平分∠ABC,A'C平分∠ACB,
∴A'M=A'N=A'P,
∴AA'平分∠BAC,
∴∠DAA'=∠EAA'.
∵A'B平分∠ABC,A'C平分∠ACB,
∴∠A'BC=$\frac{1}{2}$∠ABC,∠A'CB=$\frac{1}{2}$∠ACB.
∵∠1=125°,
∴∠A'BC+∠A'CB=180°-∠1=180°-125°=55°,
∴∠ABC+∠ACB=2(∠A'BC+∠A'CB)=110°,
∴∠BAC=180°-110°=70°.
∵将△ABC纸片沿DE折叠,点A落在点A'处,
∴DA=DA',
∴∠DAA'=∠DA'A.
∵∠DAA'=∠CAA',
∴∠DAA'=∠DA'A=∠CAA'.
∵∠2是△A'DA的一个外角,
∴∠2=∠DA'A+∠DAA'=∠DAA'+∠CAA'=∠BAC=70°.

70° [解析]如图,连接AA',过A'作A'M⊥AB,A'N⊥BC,A'P⊥AC.
∵A'B平分∠ABC,A'C平分∠ACB,
∴A'M=A'N=A'P,
∴AA'平分∠BAC,
∴∠DAA'=∠EAA'.
∵A'B平分∠ABC,A'C平分∠ACB,
∴∠A'BC=$\frac{1}{2}$∠ABC,∠A'CB=$\frac{1}{2}$∠ACB.
∵∠1=125°,
∴∠A'BC+∠A'CB=180°-∠1=180°-125°=55°,
∴∠ABC+∠ACB=2(∠A'BC+∠A'CB)=110°,
∴∠BAC=180°-110°=70°.
∵将△ABC纸片沿DE折叠,点A落在点A'处,
∴DA=DA',
∴∠DAA'=∠DA'A.
∵∠DAA'=∠CAA',
∴∠DAA'=∠DA'A=∠CAA'.
∵∠2是△A'DA的一个外角,
∴∠2=∠DA'A+∠DAA'=∠DAA'+∠CAA'=∠BAC=70°.

9 如图,在△ABC 中,BM= MC,∠ABM= ∠ACM.求证:AM 平分∠BAC.
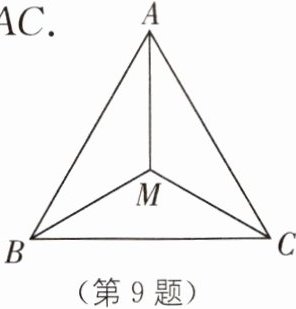

答案:
过点M作ME⊥AB,MF⊥AC,垂足分别为E,F,
∴∠BEM=∠CFM=90°.
在△BEM和△CFM中,$\left\{\begin{array}{l} ∠BEM=∠CFM,\\ ∠EBM=∠FCM,\\ BM=CM,\end{array}\right. $
∴△BEM≌△CFM(AAS),
∴ME=MF.
又ME⊥AB,MF⊥AC,
∴点M在∠BAC的平分线上,即AM平分∠BAC.
∴∠BEM=∠CFM=90°.
在△BEM和△CFM中,$\left\{\begin{array}{l} ∠BEM=∠CFM,\\ ∠EBM=∠FCM,\\ BM=CM,\end{array}\right. $
∴△BEM≌△CFM(AAS),
∴ME=MF.
又ME⊥AB,MF⊥AC,
∴点M在∠BAC的平分线上,即AM平分∠BAC.
10 如图,在∠AOB 的两边 OA,OB 上分别取 OM= ON,OD= OE,DN 和 EM 相交于点 C.求证:点 C 在∠AOB 的平分线上.
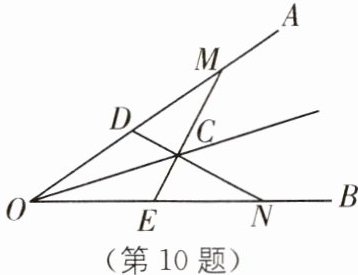

答案:
过点C作CG⊥OA,垂足为G,CF⊥OB,垂足为F.
∵OM=ON,OE=OD,∠MOE=∠NOD,
∴△MOE≌△NOD(SAS),
∴S△MOE=S△NOD,
∴S△MOE-S四边形ODCE=S△NOD-S四边形ODCE,
∴S△MDC=S△NEC.
∵OM=ON,OD=OE,
∴MD=NE.由面积法可得CG=CF.又CG⊥OA,CF⊥OB,
∴点C在∠AOB的平分线上.
∵OM=ON,OE=OD,∠MOE=∠NOD,
∴△MOE≌△NOD(SAS),
∴S△MOE=S△NOD,
∴S△MOE-S四边形ODCE=S△NOD-S四边形ODCE,
∴S△MDC=S△NEC.
∵OM=ON,OD=OE,
∴MD=NE.由面积法可得CG=CF.又CG⊥OA,CF⊥OB,
∴点C在∠AOB的平分线上.
11 如图,A,B 两点分别在射线 OM,ON 上,点 C 在∠MON 的内部,AC= BC,CD⊥OM,CE⊥ON,垂足分别为 D,E,且 AD= BE.
(1)求证:OC 平分∠MON;
(2)若 AD= 3,BO= 4,求 AO 的长.
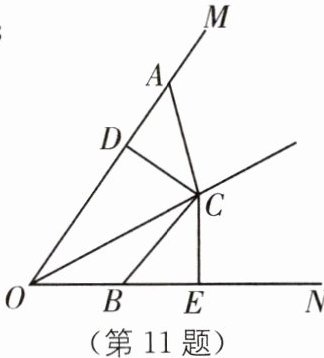
(1)求证:OC 平分∠MON;
(2)若 AD= 3,BO= 4,求 AO 的长.

答案:
(1)
∵CD⊥OM,CE⊥ON,
∴∠ADC=∠CEB=90°.
在Rt△ADC和Rt△BEC中,$\left\{\begin{array}{l} AC=BC,\\ AD=BE,\end{array}\right. $
∴Rt△ADC≌Rt△BEC(HL),
∴CD=CE.
∵CD⊥OM,CE⊥ON,
∴OC平分∠MON.
(2)
∵Rt△ADC≌Rt△BEC,AD=3,
∴BE=AD=3.
∵BO=4,
∴OE=OB+BE=4+3=7.
∵CD⊥OM,CE⊥ON,
∴∠CDO=∠CEO=90°.
在Rt△DOC和Rt△EOC中,$\left\{\begin{array}{l} OC=OC,\\ CD=CE,\end{array}\right. $
∴Rt△DOC≌Rt△EOC(HL),
∴OD=OE=7.
∵AD=3,
∴AO=OD+AD=7+3=10.
(1)
∵CD⊥OM,CE⊥ON,
∴∠ADC=∠CEB=90°.
在Rt△ADC和Rt△BEC中,$\left\{\begin{array}{l} AC=BC,\\ AD=BE,\end{array}\right. $
∴Rt△ADC≌Rt△BEC(HL),
∴CD=CE.
∵CD⊥OM,CE⊥ON,
∴OC平分∠MON.
(2)
∵Rt△ADC≌Rt△BEC,AD=3,
∴BE=AD=3.
∵BO=4,
∴OE=OB+BE=4+3=7.
∵CD⊥OM,CE⊥ON,
∴∠CDO=∠CEO=90°.
在Rt△DOC和Rt△EOC中,$\left\{\begin{array}{l} OC=OC,\\ CD=CE,\end{array}\right. $
∴Rt△DOC≌Rt△EOC(HL),
∴OD=OE=7.
∵AD=3,
∴AO=OD+AD=7+3=10.
12 等面积法 (2025·河北唐山路南区期中)如图,在△ABC 中,点 D 在边 BC 延长线上,∠ACB= 110°,∠ABC 的平分线交 AD 于点 E,过点 E 作 EH⊥BD,垂足为 H,且∠CEH= 55°.
(1)求∠ACE 的度数;
(2)求证:AE 平分∠CAF;
(3)若 AC+CD= 14,AB= 8.5,且 S△ACD= 21,求△ABE 的面积.
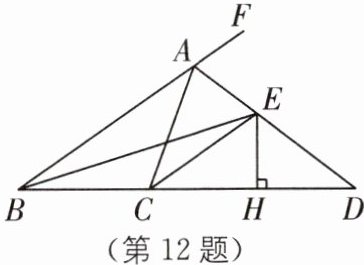
(1)求∠ACE 的度数;
(2)求证:AE 平分∠CAF;
(3)若 AC+CD= 14,AB= 8.5,且 S△ACD= 21,求△ABE 的面积.

答案:
(1)
∵EH⊥BD,
∴∠CHE=90°.
∵∠CEH=55°,
∴∠ECH=90°-55°=35°,
∴∠ACE=180°-35°-110°=35°.
(2)如图,过点E分别作EM⊥BF于点M,EN⊥AC于点N.

∵BE平分∠ABC,
∴EM=EH.
∵∠ACE=∠ECH=35°,
∴CE平分∠ACD,
∴EN=EH,
∴EM=EN,
∴AE平分∠CAF.
(3)
∵AC+CD=14,S△ACD=21,EM=EN=EH,
∴S△ACD=S△ACE+S△CED=$\frac{1}{2}$AC·EN+$\frac{1}{2}$CD·EH=$\frac{1}{2}$(AC+CD)·EM=21,
即$\frac{1}{2}$×14EM=21,解得EM=3.
∵AB=8.5,
∴S△ABE=$\frac{1}{2}$AB·EM=$\frac{1}{2}$×8.5×3=$\frac{51}{4}$.
(1)
∵EH⊥BD,
∴∠CHE=90°.
∵∠CEH=55°,
∴∠ECH=90°-55°=35°,
∴∠ACE=180°-35°-110°=35°.
(2)如图,过点E分别作EM⊥BF于点M,EN⊥AC于点N.

∵BE平分∠ABC,
∴EM=EH.
∵∠ACE=∠ECH=35°,
∴CE平分∠ACD,
∴EN=EH,
∴EM=EN,
∴AE平分∠CAF.
(3)
∵AC+CD=14,S△ACD=21,EM=EN=EH,
∴S△ACD=S△ACE+S△CED=$\frac{1}{2}$AC·EN+$\frac{1}{2}$CD·EH=$\frac{1}{2}$(AC+CD)·EM=21,
即$\frac{1}{2}$×14EM=21,解得EM=3.
∵AB=8.5,
∴S△ABE=$\frac{1}{2}$AB·EM=$\frac{1}{2}$×8.5×3=$\frac{51}{4}$.
查看更多完整答案,请扫码查看


