《2025年课时训练八年级数学上册人教版江苏人民出版社》

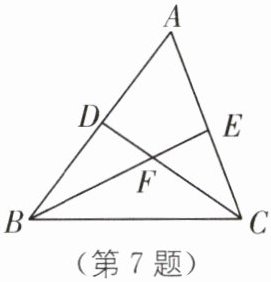
7 双角平分线模型 (2025·山东青岛市北区期末)如图,在△ABC 中,∠ABC,∠ACB 的平分线 BE,CD 相交于点 F,∠A= 58°,则∠BFC 的度数为( ).

A.118°
B.119°
C.120°
D.121°

答案： 【解析】：本题可根据三角形内角和定理求出$\angle ABC + \angle ACB$的度数，再根据角平分线的性质求出$\angle FBC + \angle FCB$的度数，最后在$\triangle BFC$中利用三角形内角和定理求出$\angle BFC$的度数。
步骤一：根据三角形内角和定理求出$\angle ABC + \angle ACB$的度数
在$\triangle ABC$中，根据三角形内角和定理：三角形的内角和为$180^{\circ}$，已知$\angle A = 58^{\circ}$，则可得：
$\angle ABC + \angle ACB = 180^{\circ} - \angle A = 180^{\circ} - 58^{\circ} = 122^{\circ}$
步骤二：根据角平分线的性质求出$\angle FBC + \angle FCB$的度数
因为$BE$平分$\angle ABC$，$CD$平分$\angle ACB$，所以$\angle FBC = \frac{1}{2}\angle ABC$，$\angle FCB = \frac{1}{2}\angle ACB$。
则$\angle FBC + \angle FCB = \frac{1}{2}(\angle ABC + \angle ACB)$，将$\angle ABC + \angle ACB = 122^{\circ}$代入可得：
$\angle FBC + \angle FCB = \frac{1}{2}×122^{\circ} = 61^{\circ}$
步骤三：在$\triangle BFC$中利用三角形内角和定理求出$\angle BFC$的度数
在$\triangle BFC$中，根据三角形内角和定理可得：
$\angle BFC = 180^{\circ} - (\angle FBC + \angle FCB)$
将$\angle FBC + \angle FCB = 61^{\circ}$代入上式可得：
$\angle BFC = 180^{\circ} - 61^{\circ} = 119^{\circ}$
【答案】：B

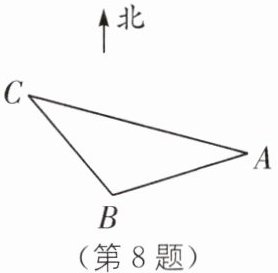
8 (2025·河南南阳方城六校联考期末)如图,C 处在 B 处的北偏西 40°方向,C 处在 A 处的北偏西 75°方向,则∠ACB 的度数为 .

答案： 【解析】：本题可根据方向角的定义求出相关角的度数，再利用三角形内角和定理求出$\angle ACB$的度数。
步骤一：根据方向角的定义求出$\angle ABC$和$\angle BAC$的度数
已知$C$处在$B$处的北偏西$40^{\circ}$方向，根据方向角的定义可知$\angle ABC = 40^{\circ}+90^{\circ}=130^{\circ}$。
已知$C$处在$A$处的北偏西$75^{\circ}$方向，根据方向角的定义可知$\angle BAC = 90^{\circ}-75^{\circ}=15^{\circ}$。
步骤二：利用三角形内角和定理求出$\angle ACB$的度数
在$\triangle ABC$中，根据三角形内角和定理：三角形内角和为$180^{\circ}$，可得$\angle ACB = 180^{\circ}-\angle ABC - \angle BAC$。
将$\angle ABC = 130^{\circ}$，$\angle BAC = 15^{\circ}$代入上式可得：
$\angle ACB = 180^{\circ}-130^{\circ}-15^{\circ}=35^{\circ}$
【答案】：$35^{\circ}$

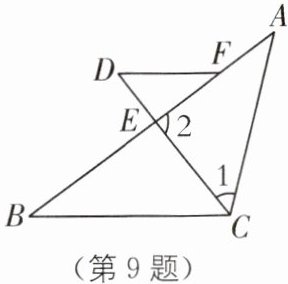
9 (2025·广东揭阳揭西期末)如图,在△ABC 中,CD 平分∠ACB,CD 交边 AB 于点 E,在边 AE 上取点 F,连接 DF,使∠1= ∠D.
(1)求证:DF//BC;
(2)当∠A= 36°,∠DFE= 34°时,求∠2 的度数.

答案：
(1)证明：
∵CD平分∠ACB，
∴∠BCD=∠2。
∵∠1=∠D，∠1=∠BCD（对顶角相等），
∴∠D=∠BCD，
∴DF//BC。
(2)解：
∵DF//BC，
∴∠B=∠DFE=34°。
在△ABC中，∠A=36°，∠B=34°，
∴∠ACB=180°-∠A-∠B=110°。
∵CD平分∠ACB，
∴∠2=∠ACB/2=55°。
答：∠2的度数为55°。

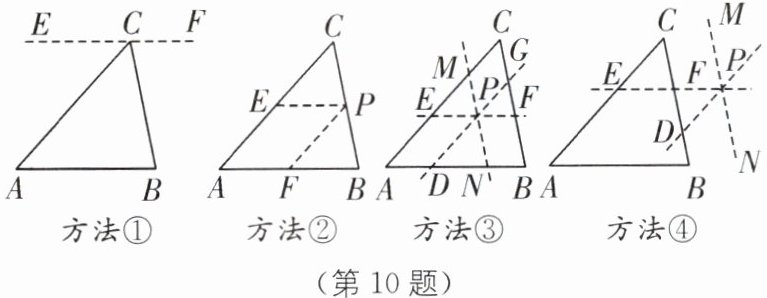
10 (2025·山东淄博张店区期中)[阅读材料]为了说明“三角形的内角和是 180°”,小明给出了如图所示的四种作辅助线的方法.
方法①:过△ABC 的顶点 C 作 EF//AB;
方法②:点 P 在△ABC 的边 BC 上,过点 P 作 PE//AB 交 AC 于点 E,PF//AC 交 AB 于点 F;
方法③:点 P 在△ABC 的内部,过点 P 作 EF//AB 交 AC,BC 于点 E,F,DG//AC 交 AB,BC 于点 D,G,MN//BC 交 AC,AB 于点 M,N;
方法④:点 P 在△ABC 的外部,过点 P 作 EF//AB 交 AC,BC 于点 E,F,DP//AC 交 BC 于点 D,MN//BC.

[解答问题](1)小明的四种作辅助线的方法中,能说明“三角形的内角和是 180°”的是 ;(只填写序号)
(2)请从你在(1)中填写的方法里选择一种方法,说明“三角形的内角和是 180°”.

答案：
(1)①②③④
(2)选择方法①证明：
证明：
∵EF//AB，
∴∠ECA=∠A（两直线平行，内错角相等），
∠FCB=∠B（两直线平行，内错角相等），
∵点E，C，F在同一条直线上，
∴∠ECA+∠ACB+∠FCB=180°（平角的定义），
∴∠A+∠ACB+∠B=180°（等量代换），
即三角形的内角和是180°。

11 中考新考法 新定义问题 (2025·安徽六安霍邱期末)在一个三角形中,如果一个内角是另一个内角的 3 倍,这样的三角形我们称之为“三倍角三角形”.例如,三个内角分别为 120°,40°,20°的三角形是“三倍角三角形”.
(1)在△ABC 中,∠A= 35°,∠B= 40°,△ABC 是“三倍角三角形”吗?为什么?
(2)若△ABC 是“三倍角三角形”,且∠B= 30°,求△ABC 中最小内角的度数.

答案：
(1)解：△ABC是“三倍角三角形”。
∵∠A=35°，∠B=40°，
∴∠C=180°-∠A-∠B=105°。
∵∠C=3∠A=105°，
∴△ABC是“三倍角三角形”。
(2)解：设最小内角的度数为x。
①当∠B是三倍角，且∠B=3x时，3x=30°，x=10°。此时第三个角为180°-30°-10°=140°，140°＞30°＞10°，符合题意。
②当∠B是较小角，且3∠B=x时，x=90°。此时第三个角为180°-30°-90°=60°，90°＞60°＞30°，最小内角为30°。
③当第三个角是三倍角，且3x=180°-30°-x时，4x=150°，x=37.5°。此时三倍角为112.5°，112.5°＞37.5°＞30°，最小内角为30°。
综上，△ABC中最小内角的度数为10°或30°。