《2025年课时训练八年级数学上册人教版江苏人民出版社》

10 (2025·南昌模拟)如图,△ABC 是等边三角形,分别以点 A 和点 C 为圆心,一定的长度为半径画弧,两弧交于 M,N 两点,连接 MN,交 AC 于点 D,又以点 C 为圆心,以 CD 的长度为半径画弧交 BC 的延长线于点 E,连接 ED 并延长交 AB 于点 F,经过此操作后,下列结论错误的是( ).

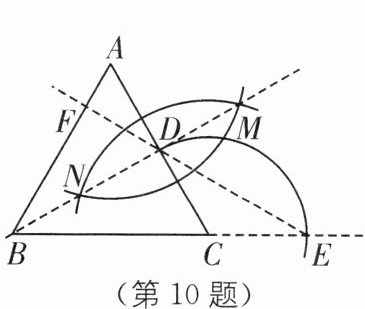
A.MN 平分∠ABC
B.∠BEF= 30°
C.CD= DF
D.BE= 2BF

答案： C

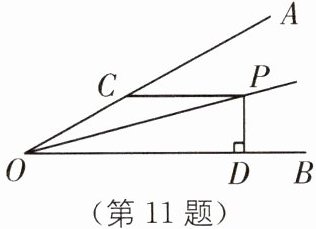
11 (2024·山东德州齐河期末)如图,已知∠AOB= 30°,P 是∠AOB 平分线上一点,CP//OB,交 OA于点 C,PD⊥OB,垂足为 D,且 PC= 7,则 PD 等于______.

答案：
$\frac{7}{2}$ [解析]如图,作PE⊥OA交OA于E.
∵CP//OB,∠AOB=30°,
∴∠PCE=∠AOB=30°.
∵PE⊥OA,
∴∠PEC=90°.
∵PC=7,
∴PE= $\frac{1}{2}$PC= $\frac{7}{2}$.
∵OP平分∠AOB,
∴∠POE=∠POD.
∵PE⊥OA,PD⊥OB,
∴PD=PE= $\frac{7}{2}$.

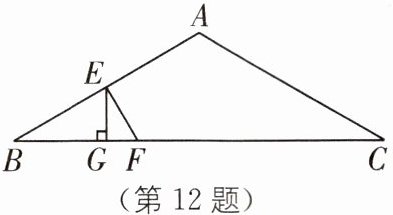
12 如图,已知 AB= AC,∠A= 120°,点 E 在 AB边上,EF 垂直平分 AB,交 BC 于点 F,EG⊥BC,垂足为 G,若 GF= 4,求 CF 的长.

答案： 连接AF.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°.
∵EF⊥AB,EG⊥BF,
∴∠BEG+∠GEF=90°,∠B+∠BEG=90°,
∴∠GEF=∠B=30°.
∵GF=4,
∴EF=2GF=8.在Rt△BEF中,BF=2EF=16.
∵EF垂直平分AB,
∴AF=BF=16,
∴∠BAF=∠B=30°,
∴∠FAC=120° - 30°=90°.又∠C=30°,
∴CF=2AF=32.

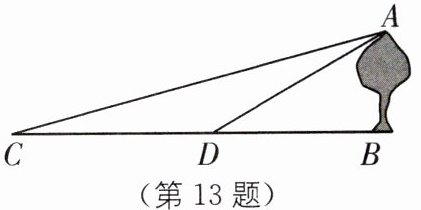
13 (2025·湖南湘西溶江中学期中)如图,树 AB 垂直于地面,为测树高,小明在 C 处,测得∠ACB= 15°,他沿 CB 方向走了 20 米,到达 D 处,测得∠ADB= 30°,你能帮助小明计算出树的高度吗？

答案：
∵∠ADB=30°,∠ACB=15°,
∴∠CAD=∠ADB - ∠ACB=15°,
∴∠ACB=∠CAD,
∴AD=CD=20.
∵∠ABD=90°,
∴AB= $\frac{1}{2}$AD=10,故树的高度为10米.

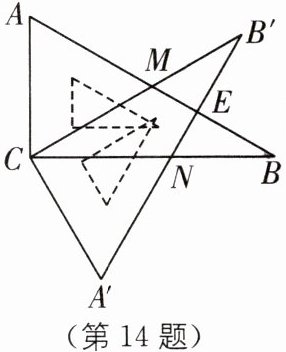
14 三角尺模型 中考新考法 操作探究 如图,含 30°角的直角三角板 ABC(∠B= 30°)绕直角顶点C 沿顺时针方向旋转 α(α＜90°),再沿∠A 的对边翻折得到△A′B′C,AB 与 B′C 交于点 M,A′B′与 BC 交于点 N,A′B′与 AB 交于点 E.
(1)求证：△ACM≌△A′CN；
(2)当 α= 30°时,找出 ME 与 MB′的数量关系,并加以说明.

答案：
(1)由翻折可得∠A=∠A',AC=A'C,∠ACM=90° - ∠MCN=∠A'CN,
∴△ACM≌△A'CN.
(2)在Rt△ABC中,
∵∠B=30°,
∴∠A=90° - 30°=60°.又α=30°,
∴∠MCN=30°,
∴∠ACM=90° - ∠MCN=60°,
∴∠EMB'=∠AMC=180° - ∠A - ∠ACM=60°.
∵∠B'=∠B=30°,
∴∠MEB'=180° - ∠EMB' - ∠B'=180° - 60° - 30°=90°,
∴MB'=2ME.