《2025年课时训练八年级数学上册人教版江苏人民出版社》

10 若 $8x^{a+5} \cdot y^{2b-3} \cdot (-0.25y^{a+5}x^{b})= -2x^{4}y^{3}$,则 $a-b$ 的值为( ).

A.-1
B.5
C.1
D.-5

答案： D

11 如图,沿大正三角形的对称轴对折,则互相重合的两个小正三角形内的单项式的乘积为______.

答案： $a$或$2a^{2}b$或$2a^{3}b$

12 计算：
(1)(2025·上海宝山区淞谊中学期中)$9x^{3}y^{3} \cdot (-\frac{1}{3}x^{2}y)^{2}+(-x^{2}y)^{3}xy^{2}$；
(2)(2025·上海长宁区西延安中学期中)$(-\frac{1}{2}a^{2}b) \cdot (-\frac{2}{5}ab^{2})-(-2ab)^{3}$.

答案：
(1)原式$=9x^{3}y^{3}× \frac{1}{9}x^{4}y^{2}-x^{6}y^{3}\cdot xy^{2}=x^{7}y^{5}-x^{7}y^{5}=0$.
(2)原式$=\frac{1}{5}a^{3}b^{3}+8a^{3}b^{3}=\frac{41}{5}a^{3}b^{3}$.

13 已知有理数 $a$,$b$,$c$ 满足 $|a-1|+(3b+1)^{2}+(c+2)^{2}= 0$,求 $(-3ab) \cdot (-a^{2}c) \cdot 6ab$ 的值.

答案： $\because |a-1|+(3b+1)^{2}+(c+2)^{2}=0$,绝对值、平方均是非负数$\therefore a=1$,$b=-\frac{1}{3}$,$c=-2$,$\therefore$原式$=18a^{4}b^{2}c=-4$.

14 新情境 数学与生活融合 某市环保局欲将一个长为 $2 × 10^{3}\ dm$,宽为 $4 × 10^{2}\ dm$,高为 $8 × 10\ dm$ 的长方体废水池中的满池废水注入正方体贮水池净化. 请你考虑一下,这些废水能否刚好装满一个正方体贮水池？若能,求该正方体贮水池的棱长；若不能,请说明理由.

答案： 能.$\because$这些废水的体积等于长方体的体积,$2× 10^{3}× 4× 10^{2}× 8× 10=64× 10^{6}=(4× 10^{2})^{3}$,$\therefore$这些废水能刚好装满一个正方体贮水池,且这个正方体的棱长为$4× 10^{2}\ dm$.

15 中考新考法 新定义问题 三角 $\triangle\begin{array}{c}a\\b\quad c\end{array} $ 表示 $3abc$,方框 $\boxed{\begin{array}{cc}x&w\\y&z\end{array} }$ 表示 $-4x^{y}w^{z}$,求 $\triangle\begin{array}{c}m\\n\quad 3\end{array} × \boxed{\begin{array}{cc}n&m\\2&5\end{array} }$.

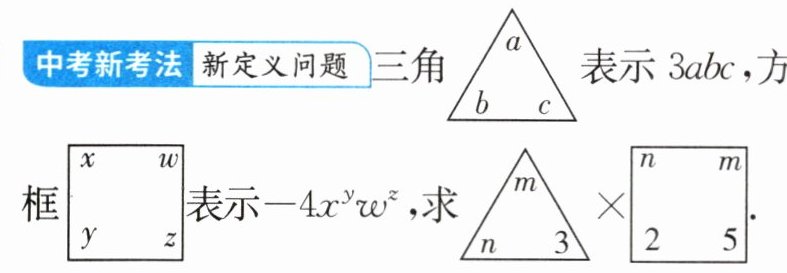
答案： $\begin{array}{r} m\\ n\quad 3\end{array} × \begin{array}{r} n\quad m\\ 2\quad 5\end{array} =9mn\cdot (-4n^{2}m^{5})=-36m^{6}n^{3}$.

16 方程思想已知 $(-2x^{m+1}y^{2n-1}) \cdot (5x^{n}y^{m})= -10x^{4}y^{4}$,求 $-2m^{2}n \cdot (-\frac{1}{2}m^{3}n^{2})^{2}$ 的值.

答案： $\because (-2x^{m+1}y^{2n-1})\cdot (5x^{n}y^{m})=-10x^{m+n+1}\cdot y^{m+2n-1}=-10x^{4}y^{4}$,$\therefore \left\{\begin{array}{l} m+n+1=4,\\ m+2n-1=4,\end{array}\right. $解得$\left\{\begin{array}{l} m=1,\\ n=2,\end{array}\right. $$\therefore -2m^{2}n\cdot \left(-\frac{1}{2}m^{3}n^{2}\right)^{2}=-\frac{1}{2}m^{8}n^{5}=-16$.