《2025年课时训练八年级数学上册人教版江苏人民出版社》

1 教材 P48 思考·变式 如图,图中是利用尺规作∠AOB 的平分线 OC 的作法,在用尺规作角平分线的过程中,用到的三角形全等的判定方法是( ).


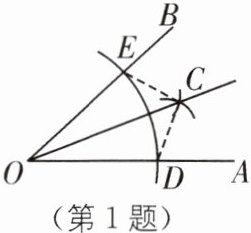
A.ASA
B.SAS
C.SSS
D.AAS

答案： C

2 教材 P48 思考·改编 (2025·广西来宾武宣期中)如图所示,已知△ABC,用直尺和圆规作∠C 的平分线 CE.(保留作图痕迹,不要求写作法)

答案：
如图所示，CE即为所求.
数学八年级上RMJY

3 教材 P49 探究·改编 (2024·青海中考)如图,OC 平分∠AOB,点 P 在 OC 上,PD⊥OB,PD= 2,则点 P 到 OA 的距离是( ).


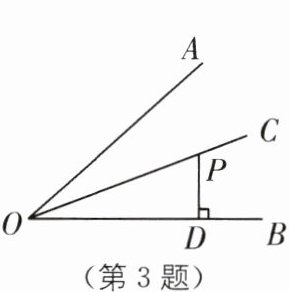
A.4
B.3
C.2
D.1

答案： C

4 教材 P49 探究·拓展 (2024·山东潍坊期末)如图,OF 平分∠AOB,FM⊥OA 于点 M,且 FM= 3,N 是射线 OB 上的一点,则 FN 的长度不可能是( ).


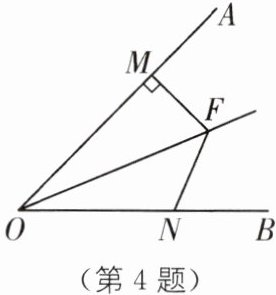
A.2
B.$\frac{10}{3}$
C.4.5
D.10

答案： A

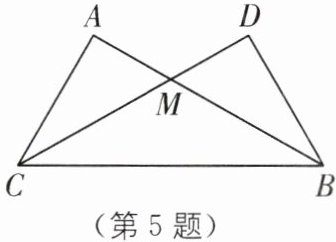
5 (2025·福建厦门集美区期末)把两个同样大小的含 30°角的直角三角尺(记作△ABC,△BCD)按如图的方式进行摆放,其中 M 是 AB 与 CD 的交点,则可以得到结论:MA 的长度等于点 M 到 BC 的距离.请用一个你学过的数学定理解释这个结论:
.

答案： 角平分线上的点到角两边的距离相等

6 教材 P48 探究·拓展 (2025·浙江温州龙湾区期中)如图(1)是一个平分角的仪器,其中 OD= OE,FD= FE.

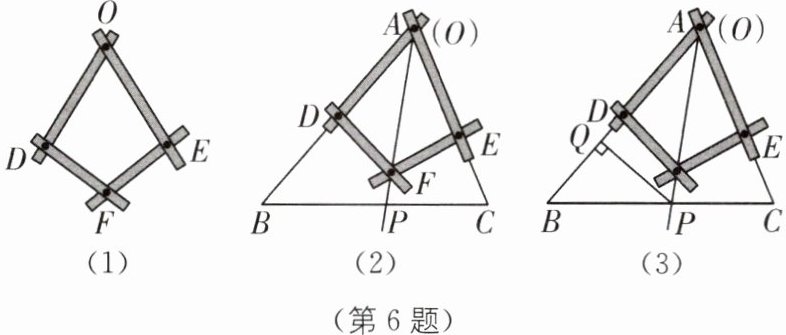
(1)如图(2),将仪器放置在△ABC 上,使点 O 与顶点 A 重合,D,E 分别在边 AB,AC 上,沿 AF 画一条射线 AP,交 BC 于点 P.AP 是∠BAC 的平分线吗?请判断并说明理由.
(2)如图(3),在(1)的条件下,过点 P 作 PQ⊥AB 于点 Q,若 PQ= 6,AC= 9,△ABC 的面积是 60,求 AB 的长.

答案：

(1)AP是∠BAC的平分线,理由如下:
在△ADF和△AEF中,$\left\{\begin{array}{l} AD=AE,\\ FD=FE,\\ AF=AF,\end{array}\right. $
$\therefore △ADF\cong △AEF(SSS),$
$\therefore ∠DAF=∠EAF,\therefore AP$平分$∠BAC.$
(2)如图,过点P作$PG⊥AC$于点G.

∵AP平分$∠BAC,PQ⊥AB,\therefore PG=PQ=6.$
$\because S_{△ABC}=S_{△ABP}+S_{△APC}=\frac {1}{2}AB\cdot PQ+\frac {1}{2}AC\cdot PG,$
$\therefore \frac {1}{2}AB×6+\frac {1}{2}×9×6=60,\therefore AB=11.$