《2025年课时训练八年级数学上册人教版江苏人民出版社》

1 教材 P45 习题 T11·拓展 如图,在△ABC 中,AD⊥BC 于点 D,根据“HL”判定△ABD≌△ACD,还需添加条件( ).

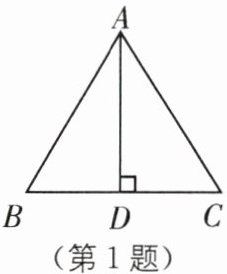
A.AB= AC
B.CD= BD
C.∠BAD= ∠CAD
D.∠C= ∠B

答案： A

2 教材 P43 练习 T1·变式 如图,点 B,C(O),E 在同一条直线上,∠B= ∠E= 90°,AB= CE,请添加一个适当的条件______,使得△ABC≌△OEF(只需写一个,不添加辅助线).

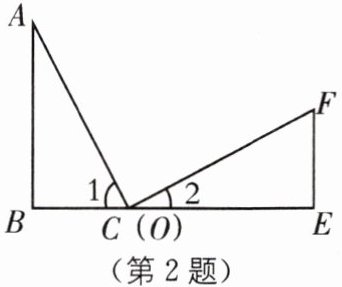
答案： AC=OF(答案不唯一)

3 教材 P42 例 6·改编 如图,AD,BC 相交于点 O,BC= AD,∠C= ∠D= 90°,求证:△ACB≌△BDA.

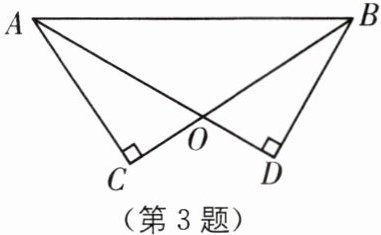
答案： 在Rt△ACB和Rt△BDA中，{BC=AD,AB=BA}
∴Rt△ACB≌Rt△BDA(HL).

4 (2025·广东广州华南师大附中期未)如图,已知 AB⊥CD,ED⊥CD,垂足分别为 B,D,且 EC= CA,ED= CB.求证:△EDC≌△CBA.

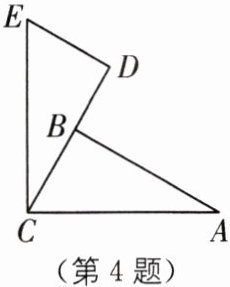
答案：
∵AB⊥CD,ED⊥CD,
∴∠D=∠ABC=90°. 在Rt△EDC和Rt△CBA中，{EC=CA,ED=CB}
∴Rt△EDC≌Rt△CBA(HL).

5 新情境 测量孔子雕像的宽度 (2025·山东淄博张店区重庆路中学期中改编)山东曲阜是孔子的故乡,在曲阜博物馆广场中央矗立着地标性建筑孔子雕像,总高 27 米,A,B 两点分别为雕像底座的两端(其中 A,B 两点均在地面上).因为 A,B 两点间的实际距离无法直接测量,甲同学设计出了如下方案:如图,先确定直线 AB,过点 B 作直线 BE,在直线 BE 上找可以直接到达点 A 的一点 D,连接 DA,作 DC= DA,交直线 AB 于点 C,最后测量 BC 的长即可.
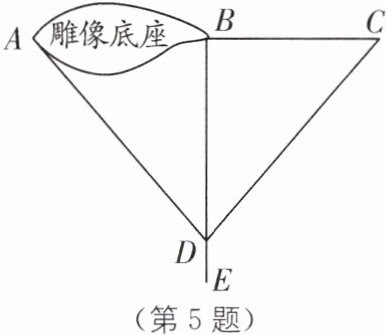
甲同学的方案可行吗?______(填“可行”或“不可行”).若方案可行说明理由,若方案不可行,请添加一个使该方案可行的条件:______,并说明你添加条件后可行的理由.

答案： 不可行　DB⊥AC 理由:
∵DB⊥AC,
∴∠ABD=∠CBD=90°.
∵DA=DC,DB=DB,
∴Rt△DBA≌Rt△DBC(HL),
∴AB=CB.

6 教材 P43 练习 T1·拓展 如图所示,有两个长度相同的滑梯 BC 和 EF,CA⊥BF,ED⊥BF,垂足分别为 A,D,左边滑梯的高度 AC 与右边滑梯水平方向的长度 DF 相等.问:两个滑梯的倾斜角∠ABC 和∠DFE 的大小有什么关系?

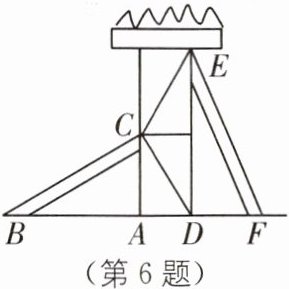
答案： ∠ABC+∠DFE=90°.理由如下: 由题意，可得△ABC与△DEF均是直角三角形，且BC=EF,AC=DF. 在Rt△ABC和Rt△DEF中，{BC=EF,AC=DF}
∴Rt△ABC≌Rt△DEF(HL),
∴∠ABC=∠DEF.
∵∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.