《2025年课时训练八年级数学上册人教版江苏人民出版社》

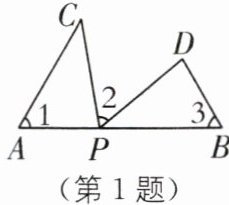
1 如图,若点A,P,B在一条直线上,∠1= ∠2= ∠3,PC= PD.求证:△APC≌△BDP,AB= AC+BD.

答案：
∵∠CPB是△APC的外角,
∴∠CPB=∠1+∠C.
∵∠CPB=∠2+∠BPD,∠1=∠2,
∴∠C=∠BPD.
在△APC和△BDP中，∠C=∠BPD，
∠1=∠3，
PC=DP，
∴△APC≌△BDP(AAS)，
∴AC=BP,AP=BD.
∵AB=AP+BP,
∴AB=BD+AC.

变式1.1 如图,在△ABC中,∠ACB= 90°,AC= BC,BE⊥CE于点E,AD⊥CE于点D,DE= 5,AD= 9,则BE的长是( ).


A.6
B.5
C.4.5
D.4

答案： D

变式1.2 如图,△ABC为等腰直角三角形,AC= BC,AC⊥BC,A(0,3),C(1,0),求点B的坐标.

答案：
如图,过点B作BD⊥x轴于点D.

∵BD⊥x轴于点D,
∴∠AOC=∠CDB=90°.
∵∠ACB=90°,
∴∠ACO+∠BCD=90°.
∵∠ACO+∠OAC=90°,
∴∠OAC=∠BCD.
在△AOC和△CDB中，∠AOC=∠CDB，
∠OAC=∠BCD，
AC=BC，
∴△AOC≌△CDB(AAS),
∴CD=AO,OC=BD.
∵C(1,0),A(0,3)，
∴OC=1,OA=3,
∴BD=1,CD=3，
∴OD=4,
∴点B的坐标为(4,1).

2 如图,已知AD是△ABC中BC边上的中线,AB= 5,AC= 3,则AD的取值范围是( ).


A.2＜AD＜8
B.1＜AD＜4
C.2＜AD＜5
D.4≤AD≤8

答案：
B [解析]如图,延长AD到点E,使DE=AD,连接CE.

在△ECD和△ABD中，
CD=BD，
∠CDE=∠BDA，
DE=AD，
∴△ECD≌△ABD(SAS)，
∴EC=AB=5.
∵CE - AC ＜ AE ＜ CE + AC,
∴5 - 3 ＜ AE ＜ 5 + 3,即2 ＜ 2AD ＜ 8,
∴1 ＜ AD ＜ 4.故选B.

变式2.1 已知AD是△ABC中BC边上的中线,若AB= 3,AD= 2,则AC的长可以是( ).

A.6
B.7
C.8
D.9

答案： A

变式2.2 如图,已知AC= DE,点B是DC中点,求证:∠DEB= ∠A.

答案：
如图,延长EB到点F，使BF=EB,连接FC.

∵点B是DC中点，
∴BD=BC.
在△BED和△BFC中，
BE=BF，
∠DBE=∠CBF，
BD=BC，
∴△BED≌△BFC(SAS)，
∴DE=CF,∠DEB=∠F.
∵AC=DE,
∴AC=CF,
∴∠A=∠F,
∴∠DEB=∠A.

3 如图,在四边形ABDC中,∠D= ∠ABD= 90°,点O为BD的中点,AB+CD= AC.
(1)求证:CO平分∠ACD;
(2)求证:AO平分∠BAC,OA⊥OC.

答案：

(1)如图,延长AO交CD的延长线于点E.

∵∠CDB=∠ABD=90°，
∴∠CDB+∠ABD=180°，
∴AB//CE,
∴∠BAO=∠E.
在△ABO和△EDO中，
∠BAO=∠E，
∠AOB=∠EOD，
OB=OD，
∴△ABO≌△EDO(AAS)，
∴AO=OE,AB=DE.
∵AC=AB+CD,CE=CD+DE=CD+AB，
∴CA=CE.
∵OA=OE,OC=OC,
∴△ACO≌△ECO(SSS)，
∴∠ACO=∠ECO,
∴CO平分∠ACD.
(2)
∵△ACO≌△ECO,
∴∠CAE=∠E.
∵∠E=∠BAE,
∴∠CAE=∠BAE，
∴AO平分∠CAB.
∵△ACO≌△ECO,
∴∠AOC=∠EOC=90°，
∴CO⊥AO.