《2025年实验班提优训练八年级数学上册人教版》

20. 中考新考法 新定义问题 (2025·吉林永吉期末)阅读 材料.
对数的创始人是苏格兰数学家纳皮尔 (1550—1617年),纳皮尔发明对数是在指 数书写方式之前,直到18世纪瑞士数学家 欧拉(1707—1783年)才发现指数与对数之 间的联系.
对数的定义:一般地,若$a^{x}= N(a＞0,a≠$ 1),那么x叫作以a为底N的对数,记作 $x= log_{a}N$,比如指数式$2^{3}= 8$可以转化为对 数式$3= log_{2}8$,对数式$4= log_{3}81$可以转化 为指数式$3^{4}= 81$.我们根据对数的定义可得 到对数的一个性质为$log_{a}(M\cdot N)= $ $log_{a}M+log_{a}N(a＞0,a≠1,M＞0,N＞0).$ 理由如下：
设$log_{a}M= m,log_{a}N= n$,则$M= a^{m},N= $ $a^{n},\therefore M\cdot N= a^{m}\cdot a^{n}= a^{m+n},$
由对数的定义,得$m+n= log_{a}(M\cdot N),$
又$m+n= log_{a}M+log_{a}N,$
$\therefore log_{a}(M\cdot N)= log_{a}M+log_{a}N.$
请你仔细阅读上面的材料,解答下列问题.
(1)将指数式$5^{3}= 125$转化为对数式 为 $3 = log_5 125$;
(2)计算:$log_{2}32= $5;
(3)求证:$log_{a}\frac {M}{N}= log_{a}M-log_{a}N(a＞0,$
$a≠1,M＞0,N＞0);$
设$log_a M = m$，$log_a N = n$，则$M = a^m$，$N = a^n$，$\therefore \frac{M}{N} = \frac{a^m}{a^n} = a^{m - n}$，由对数的定义得$m - n = log_a \frac{M}{N}$。又$m - n = log_a M - log_a N$，$\therefore log_a \frac{M}{N} = log_a M - log_a N$。
(4)直接写出$log_{3}2+log_{3}6-log_{3}4$的值.1

答案： $(1)3 = log_5 125(2)5 [$解析]
∵$2^5 = 32,$
∴$log_2 32 = 5.(3)$设log_a M = m,log_a N = n,则M = a^m,N = a^n,
∴M/N = a^m/a^n=a^(m - n),由对数的定义得m - n = log_a M/N.又m - n = log_a M - log_a N,
∴$log_a M/N = log_a M - log_a N.(4)log_3 2 + log_3 6 - log_3 4 = log_3 (2×6/4)=log_3 3 = 1.$

21. 中考新考法 解题方法型阅读理解题 (2025·江苏南通 崇川区期中)我们学过单项式除以单项式、多项 式除以单项式,那么多项式除以多项式该怎 么计算呢? 我们也可以用竖式进行类似演 算,即先把被除式、除式按某个字母降幂排 列,并把所缺的项用零补齐(或留出空白), 再类似于数的竖式除法求出商式和余式,其 中余式为0或余式的次数低于除式的次数. 例如:计算$(8x^{2}+6x+2)÷(2x+1)$,可用 如图的竖式进行计算.因此商式是$4x+1,$ 余式是1.
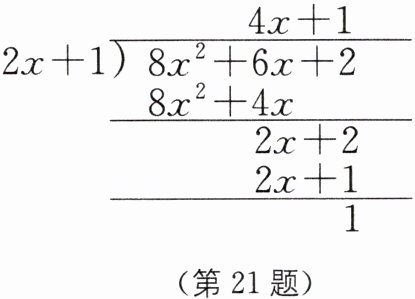
(1)计算$(3x^{2}+10x+4)÷(x+3)$,商式是 _ ,余式是 _ ;
(2)计算$(a^{2}+ab-2b^{2})÷(a-b)$的结果 为 _ ;
(3)已知M是一个整式,m是常数,$x≠-1,$ $M(x+1)= x^{2}+mx+36$,求m的值.

答案：

(1)3x + 1 1 [解析]列竖式计算如下:

∴商式是3x + 1,余式是1.
(2)a + 2b [解析]列竖式计算如下:

∴$(a^2 + ab - 2b^2)÷(a - b)=a + 2b.(3)$
∵M是一个整式,m是常数$,x≠ - 1,M(x + 1)=x^2 + mx + 36,$
∴$M=(x^2 + mx + 36)÷(x + 1).$列竖式计算如下:

∵M是一个整式,
∴37 - m = 0,
∴m = 37.